题目内容
 (2012•深圳二模)如图,已知正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形A′B′C′D′,其中A与A'重合,且BB′<DD′<CC′.
(2012•深圳二模)如图,已知正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形A′B′C′D′,其中A与A'重合,且BB′<DD′<CC′.(1)证明AD′∥平面BB′C′C,并指出四边形AB′C′D′的形状;
(2)如果四边形中AB′C′D′中,AD′=
| 2 |
| 5 |
| 6 |
分析:(1)先证明BB°∥CC′∥DD′,在CC′上取点E,使得CE=DD′,连接BE,D′E,证明ABED′是平行四边形,可得AD′∥BE,从而可证AD′平面BB′C′C,四边形AB′C′D′是平行四边形;
(2)先证明AC′⊥B′C′,根据正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形A′B′C′D′,可得平面ABCD与平面AB′C′D′所成的锐二面角θ的余弦值=
,计算面积即可求得结论.
(2)先证明AC′⊥B′C′,根据正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形A′B′C′D′,可得平面ABCD与平面AB′C′D′所成的锐二面角θ的余弦值=
| SAB′C′D′ |
| SABCD |
解答:(1)证明:依题意,BB′⊥平面AB′C′D′,CC′⊥平面AB′C′D′,DD′⊥平面AB′C′D′,
所以BB°∥CC′∥DD′. …(2分)
在CC′上取点E,使得CE=DD′,
连接BE,D′E,如图1.
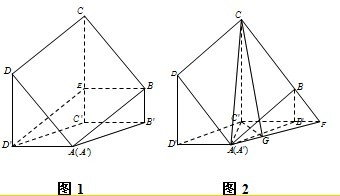
因为CE∥DD′,且CE=DD′,所以CDD′E是平行四边形,∴D′E∥DC,且D′E=DC.
又ABCD是正方形,∴DC∥AB,且DC=AB,
所以D′E∥AB,且D′E=AB,故ABED′是平行四边形,…(4分)
从而AD′∥BE,又BE?平面BB′C′C,AD′?平面BB′C′C,
所以AD′∥平面BB′C′C. …(6分)
四边形AB′C′D′是平行四边形.…(7分)
(2)依题意,在Rt△ABB′中,BB′=1,在Rt△ADD′中,DD′=2,
所以CC′=BB′+DD′-AA′=1+2-0=3. …(8分)
连接AC,AC′,如图2,
在Rt△ACC′中,AC′=
.
所以AC′2+B′C′2=AB′2,故AC′⊥B′C′.…(10分)
由题意,正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形A′B′C′D′,
所以平面ABCD与平面AB′C′D′所成的锐二面角θ的余弦值=
. …(12分)
而SABCD=6,SAB′C′D′=B′C′×AC′=
×
,所以cosθ=
,
所以平面ABCD与平面AB′C′D′所成的锐二面角θ的余弦值为
. …(14分)
所以BB°∥CC′∥DD′. …(2分)
在CC′上取点E,使得CE=DD′,
连接BE,D′E,如图1.

因为CE∥DD′,且CE=DD′,所以CDD′E是平行四边形,∴D′E∥DC,且D′E=DC.
又ABCD是正方形,∴DC∥AB,且DC=AB,
所以D′E∥AB,且D′E=AB,故ABED′是平行四边形,…(4分)
从而AD′∥BE,又BE?平面BB′C′C,AD′?平面BB′C′C,
所以AD′∥平面BB′C′C. …(6分)
四边形AB′C′D′是平行四边形.…(7分)
(2)依题意,在Rt△ABB′中,BB′=1,在Rt△ADD′中,DD′=2,
所以CC′=BB′+DD′-AA′=1+2-0=3. …(8分)
连接AC,AC′,如图2,
在Rt△ACC′中,AC′=
| 3 |
所以AC′2+B′C′2=AB′2,故AC′⊥B′C′.…(10分)
由题意,正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形A′B′C′D′,
所以平面ABCD与平面AB′C′D′所成的锐二面角θ的余弦值=
| SAB′C′D′ |
| SABCD |
而SABCD=6,SAB′C′D′=B′C′×AC′=
| 2 |
3=
|
| ||
| 6 |
所以平面ABCD与平面AB′C′D′所成的锐二面角θ的余弦值为
| ||
| 6 |
点评:本题考查线面平行,考查面面角,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
