题目内容
 如图,已知正方形ABCD的边长为1,过正方形中心O的直线MN分别交正方形的边AB,CD于M,N,则当
如图,已知正方形ABCD的边长为1,过正方形中心O的直线MN分别交正方形的边AB,CD于M,N,则当| MN |
| BN |
| ||
| 2 |
| ||
| 2 |
分析:通过三角形的全等,求出x的值,利用方程有解,推出t的范围,然后求解即可求得结论.
解答:解:易证△AOM≌△CON,则AM=CN=x
设CN=x,经过点N作NE⊥AB
则四边形NEBC为矩形
∴NE=BC=1,BE=CN=x
则ME=(1-x)-x=1-2x(或2x-1)
∴MN2=EM2+EN2=2-4x+4x2
BN2=BC2+CN2=1+x2
令2-4x+4x2=t(1+x2),整理
﹙t-4﹚x2+4x+t-2=0有实根
∴16-4(t-4)(t-2)≧0
解得:3-
≤t≤3+
∴当
取最小值时,
即t取最小值3-
,x=
即CN=
,
故答案为:
设CN=x,经过点N作NE⊥AB
则四边形NEBC为矩形
∴NE=BC=1,BE=CN=x
则ME=(1-x)-x=1-2x(或2x-1)
∴MN2=EM2+EN2=2-4x+4x2
BN2=BC2+CN2=1+x2
令2-4x+4x2=t(1+x2),整理
﹙t-4﹚x2+4x+t-2=0有实根
∴16-4(t-4)(t-2)≧0
解得:3-
| 5 |
| 5 |
∴当
| MN |
| BN |
即t取最小值3-
| 5 |
| ||
| 2 |
即CN=
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查学生分析解决问题的能力,考查学生的探究能力,属于中档题.

练习册系列答案
相关题目
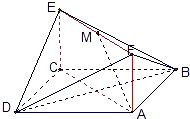 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB= 如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF=
如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF= 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直, (2012•深圳二模)如图,已知正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形A′B′C′D′,其中A与A'重合,且BB′<DD′<CC′.
(2012•深圳二模)如图,已知正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形A′B′C′D′,其中A与A'重合,且BB′<DD′<CC′.