题目内容
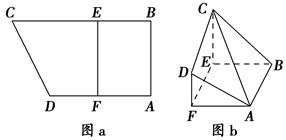
如图甲,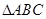 是边长为6的等边三角形,
是边长为6的等边三角形, 分别为
分别为 靠近
靠近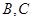 的三等分点,点
的三等分点,点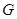 为边
为边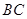 边的中点,线段
边的中点,线段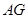 交线段
交线段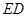 于点
于点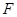 .将
.将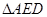 沿
沿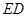 翻折,使平面
翻折,使平面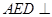 平面
平面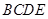 ,连接
,连接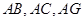 ,形成如图乙所示的几何体.
,形成如图乙所示的几何体.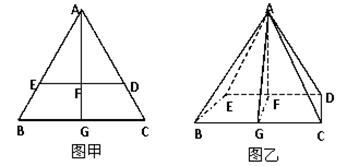
(1)求证: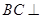 平面
平面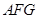
(2)求四棱锥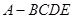 的体积.
的体积.
(1)证明过程详见试题解析;(2)四棱锥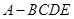 的体积为10.
的体积为10.
解析试题分析:(1)先证明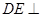 平面
平面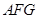 ,又
,又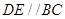 ,所以
,所以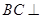 平面
平面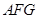 ;
;
(2)先求出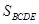 ,再用体积公式求解即可.
,再用体积公式求解即可.
试题解析:(1)在图甲中,由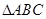 为等边三角形,
为等边三角形,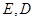 分别为三等分点,点
分别为三等分点,点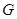 为边
为边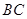 边的中点,知
边的中点,知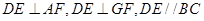 , 则在图乙中仍有
, 则在图乙中仍有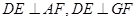 ,且
,且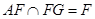 ,
,
所以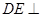 平面
平面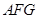 ,又
,又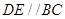 ,所以
,所以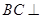 平面
平面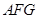 . 6分
. 6分
(2)∵平面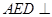 平面
平面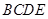 ,
,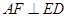 ,∴
,∴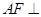 平面
平面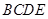 ,
,
∴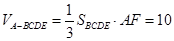 12分
12分
考点:直线与平面垂直的判定定理、空间几何体的体积.

练习册系列答案
相关题目

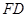 垂直于矩形
垂直于矩形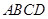 所在平面,
所在平面,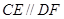 ,
, .
.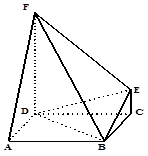
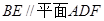 ;
; 的一个边
的一个边 ,
, ,则另一边
,则另一边 的长为何值时,三棱锥
的长为何值时,三棱锥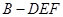 的体积为
的体积为 ?
? ,底面
,底面 是等腰梯形,且
是等腰梯形,且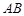 ∥
∥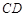 ,
, 是
是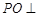 平面
平面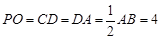 ,
,  是
是 中点.
中点.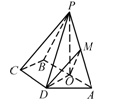
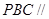 平面
平面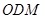 ;(2)求点
;(2)求点 到平面
到平面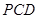 的距离.
的距离. 平面ABC.
平面ABC.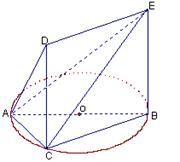
 ;
; ,
, ,
, ,试求该简单组合体的体积V.
,试求该简单组合体的体积V.
 A1B1C1中,D,E分别是AB,BB1的中点.
A1B1C1中,D,E分别是AB,BB1的中点.
 ,求三棱锥C
,求三棱锥C A1B1C1中,∠BAC=90°,AB=AC=
A1B1C1中,∠BAC=90°,AB=AC= ,AA1=3,D是BC的中点,点E在棱BB1上运动.
,AA1=3,D是BC的中点,点E在棱BB1上运动.
 A1B1E的体积.
A1B1E的体积.