题目内容
【题目】已知数列{an}的前n项和Sn满足2an=2+Sn．
（1）求证：数列{an}是等比数列；
（2）设bn=log2a2n+1，求数列{bn}的前n项和Tn．
【答案】（1）见解析；（2）
【解析】
（1）运用数列的递推式和等比数列的定义，即可得证；
（2）运用等比数列的通项公式和等差数列的求和公式，计算即可得到所求和．
（1）证明：数列{an}的前n项和Sn满足2an=2+Sn，
可得2a1=2+S1=2+a1，解得a1=2；
n≥2时，2an-1=2+Sn-1，又2an=2+Sn，
相减可得2an-2an-1=2+Sn-2-Sn-1=an，
即an=2an-1，可得数列{an}是首项、公比均为2的等比数列；
（2）由（1）可得an=2n，
bn=log2a2n+1=log222n+1=2n+1，
数列{bn}的前n项和Tn=
（3+2n+1）n=n2+2n．
练习册系列答案
阅读快车系列答案
相关题目
【题目】越接近高考学生焦虑程度越强，四个高三学生中大约有一个有焦虑症，经有关机构调查，得出距离高考周数与焦虑程度对应的正常值变化情况如下表周数
周数x | 6 | 5 | 4 | 3 | 2 | 1. |
正常值y | 55 | 63 | 72 | 80 | 90 | 99 |
其中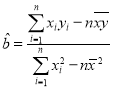
，
，
，
（1）作出散点图；
（2）根据上表数据用最小二乘法求出y关于x的线性回方程
（精确到0.01）
（3）根据经验观测值为正常值的0.85～1.06为正常，若1.06～1.12为轻度焦虑，1.12～1.20为中度焦虑，1.20及以上为重度焦虑。若为中度焦虑及以上，则要进行心理疏导。若一个学生在距高考第二周时观测值为103，则该学生是否需要进行心理疏导？
