题目内容
【题目】如图,三棱柱ABC-A1B1C1中,AB=AA1=![]() ,AC=2,∠BAC=∠A1AC=45°,∠BAA1=60°,F为棱AC的中点,E在棱BC上,且BE=2EC.
,AC=2,∠BAC=∠A1AC=45°,∠BAA1=60°,F为棱AC的中点,E在棱BC上,且BE=2EC.
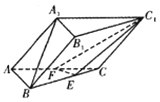
(Ⅰ)求证:A1B∥平面EFC1;
(Ⅱ)求三棱柱ABC-A1B1C1的体积.
【答案】(Ⅰ)见解析;(Ⅱ)1
【解析】
(Ⅰ)法一:连接A1C交C1F于D,连接DE,推导出A1B∥DE,由此能证明A1B∥平面EFC1;法二:取BE的中点D,取B1C1的靠近B1的三等分点D1,连接AD、A1D1、D1B、D1D,推导出四边形B1D1DB为平行四边形,四边形AA1D1D为平行四边形,从而EF∥AD,A1D1∥EF,四边形C1D1BE为平行四边形,从而D1B∥C1E,进而平面A1D1B∥平面EFC1,由此能证明A1B∥平面EFC1;(Ⅱ)连接A1F,BF,推导出A1F是三棱柱ABC-A1B1C1的高.由此能求出三棱柱ABC-A1B1C1的体积.
(Ⅰ)法一:连接A1C交C1F于D,连接DE,
因为![]() =
=![]() =
=![]() ,所以A1B∥DE,
,所以A1B∥DE,
又A1B平面EFC1,DE平面EFC1,
所以A1B∥平面EFC1.
法二:如图所示,
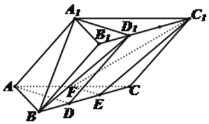
取BE的中点D,取B1C1的靠近B1的三等分点D1,连接AD、A1D1、D1B、D1D,因为B1D1∥BD,且B1D1=BD,所以四边形B1D1DB为平行四边形,
所以DD1∥BB1,又因为AA1∥BB1,所以AA1∥1,
又AA1=BB1=DD1,所以四边形AA1D1D为平行四边形,
所以A1D1∥AD,又EF为△CAD的中位线,所以EF∥AD,
所以A1D1∥EF,
因为C1D1=BE,C1D1∥BE,所以四边形C1D1BE为平行四边形,所以D1B∥C1E,
又因为A1D1平面A1D1B,BD1平面A1D1B,EF平面EFC1,C1E平面EFC1,
A1D1∩D1B=D1,EF∩C1E=E,所以平面A1D1B∥平面EFC1,
又A1B平面A1D1B,所以A1B∥平面EFC1,
(Ⅱ)连接A1F,BF,由AB=AA1=![]() ,AF=1,∠BAC=∠A1AC=45°,
,AF=1,∠BAC=∠A1AC=45°,
由余弦定理可得:A1F=BF=1,又∠BAA1=60°,所以A1B=![]() ,
,
所以由勾股定理可得A1F⊥AC,A1F⊥BF,
又BF∩AC=F,且BF平面ABC,AC平面ABC,
所以A1F⊥平面ABC,所以A1F是三棱柱ABC-A1B1C1的高.
又![]() =1,
=1,
所以三棱柱ABC-A1B1C1的体积:V=S△ABC×A1F=1×1=1.

【题目】为预防![]() 病毒爆发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于
病毒爆发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于![]() %,则认为测试没有通过),公司选定
%,则认为测试没有通过),公司选定![]() 个流感样本分成三组,测试结果如下表:
个流感样本分成三组,测试结果如下表:
|
|
| |
疫苗有效 |
|
|
|
疫苗无效 |
|
|
|
已知在全体样本中随机抽取![]() 个,抽到
个,抽到![]() 组疫苗有效的概率是
组疫苗有效的概率是![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)现用分层抽样的方法在全体样本中抽取![]() 个测试结果,问应在
个测试结果,问应在![]() 组抽取多少个?
组抽取多少个?
(Ⅲ)已知![]() ,
,![]() ,求不能通过测试的概率.
,求不能通过测试的概率.