题目内容
3.证明:C$\left.\begin{array}{l}{0}\\{n}\end{array}\right.$+$\frac{1}{2}$C$\left.\begin{array}{l}{1}\\{n}\end{array}\right.$+$\frac{1}{3}$C$\left.\begin{array}{l}{2}\\{n}\end{array}\right.$+…+$\frac{1}{k}$C$\left.\begin{array}{l}{k-1}\\{n}\end{array}\right.$+…+$\frac{1}{n+1}$C$\left.\begin{array}{l}{n}\\{n}\end{array}\right.$=$\frac{1}{n+1}$(2n+1-1).分析 利用组合数的性质,化$\frac{1}{k}$${C}_{n}^{k-1}$=$\frac{1}{n+1}$${C}_{n+1}^{k}$,代入题目中等式的左边,即可得出右边.
解答 证明:∵$\frac{1}{k}$${C}_{n}^{k-1}$=$\frac{1}{k}$•$\frac{n!}{(k-1)!•(n-k+1)!}$
=$\frac{n!}{k!•(n+1-k)!}$
=$\frac{1}{n+1}$•$\frac{(n+1)!}{k!•(n+1-k)!}$
=$\frac{1}{n+1}$${C}_{n+1}^{k}$,
∴C$\left.\begin{array}{l}{0}\\{n}\end{array}\right.$+$\frac{1}{2}$C$\left.\begin{array}{l}{1}\\{n}\end{array}\right.$+$\frac{1}{3}$C$\left.\begin{array}{l}{2}\\{n}\end{array}\right.$+…+$\frac{1}{k}$C$\left.\begin{array}{l}{k-1}\\{n}\end{array}\right.$+…+$\frac{1}{n+1}$C$\left.\begin{array}{l}{n}\\{n}\end{array}\right.$
=$\frac{1}{n+1}$•${C}_{n+1}^{1}$+$\frac{1}{n+1}$•${C}_{n+1}^{2}$+$\frac{1}{n+1}$•${C}_{n+1}^{3}$+…+$\frac{1}{n+1}$•${C}_{n+1}^{k}$+…+$\frac{1}{n+1}$•${C}_{n+1}^{n+1}$
=$\frac{1}{n+1}$•(${C}_{n+1}^{1}$+${C}_{n+1}^{2}$+${C}_{n+1}^{3}$+…+${C}_{n+1}^{k}$+…+${C}_{n+1}^{n+1}$)
=$\frac{1}{n+1}$(2n+1-1).
点评 本题考查了组合数公式的应用问题,也考查了二项式定理的应用问题,是中档题目.

| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
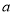 和
和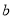 两数之间插入5个数,使他们与
两数之间插入5个数,使他们与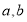 组成等差数列,则该数列的公差为( )
组成等差数列,则该数列的公差为( )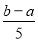 B.
B.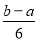 C.
C.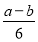 D.
D.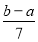
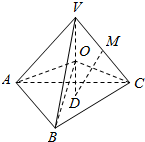 如图所示,正四面体V-ABC的高VD的中点为O,VC的中点为M.
如图所示,正四面体V-ABC的高VD的中点为O,VC的中点为M.