题目内容
(本小题满分10分)
已知数列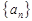 的前
的前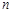 项和为
项和为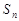 ,
,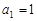 ,且
,且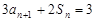 (
(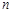 为正整数).
为正整数).
(Ⅰ)求数列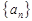 的通项公式;
的通项公式;
(Ⅱ)记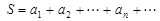 .
. 若对任意正整数
若对任意正整数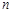 ,
,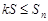 恒成立,求实数
恒成立,求实数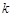 的最大值.
的最大值.
已知数列
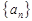 的前
的前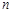 项和为
项和为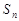 ,
,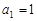 ,且
,且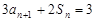 (
(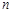 为正整数).
为正整数).(Ⅰ)求数列
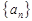 的通项公式;
的通项公式;(Ⅱ)记
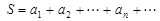 .
. 若对任意正整数
若对任意正整数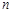 ,
,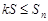 恒成立,求实数
恒成立,求实数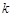 的最大值.
的最大值.(1)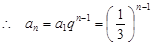 ;(2)实数
;(2)实数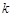 的最大值为
的最大值为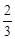 .
.
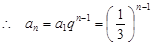 ;(2)实数
;(2)实数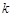 的最大值为
的最大值为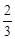 .
.(1)
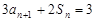 考查数列中
考查数列中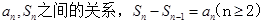 ;
;(2)
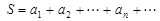 极限思想,
极限思想,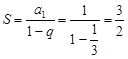 ,
,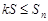 恒成立,即是
恒成立,即是 ,分离参数
,分离参数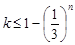 ,在最值处成立即可。
,在最值处成立即可。解:(Ⅰ)
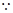
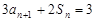 , ①
, ①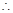 当
当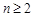 时,
时,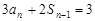 . ②
. ②由 ① - ②,得
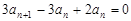 .
.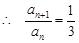
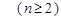 . …… 3分
. …… 3分又
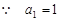 ,
,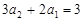 ,解得
,解得 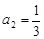 . …… 4分
. …… 4分 数列
数列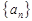 是首项为1,公比为
是首项为1,公比为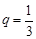 的等比数列.
的等比数列.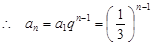 (
(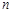 为正整数). …… 5分
为正整数). …… 5分(Ⅱ)由(1)知,
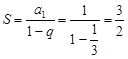 , …… 8分
, …… 8分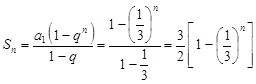 . …… 10分
. …… 10分由题意可知,对于任意的正整数
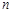 ,恒有
,恒有 ,解得
,解得 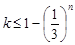 .
.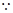 数列
数列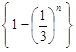 单调递增,
单调递增,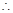 当
当 时,数列中的最小项为
时,数列中的最小项为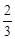 ,
,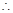 必有
必有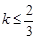 ,即实数
,即实数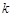 的最大值为
的最大值为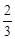 . …… 10分
. …… 10分
练习册系列答案
相关题目
 的第1项
的第1项 ,且
,且 .
. ,
,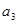 ,
, ;
; 的表达式,并用数学归纳法进行证明.
的表达式,并用数学归纳法进行证明. ,如果存在一个正整数
,如果存在一个正整数 ,使得对任意的
,使得对任意的
 都有
都有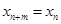 成立,那么就把这样一类数列
成立,那么就把这样一类数列 时,
时, 的周期数列;当
的周期数列;当 时,
时, 是周期为
是周期为 的周期数列。设数列
的周期数列。设数列 满足
满足
 .
. 的周期数列,则常数
的周期数列,则常数 的值是 ;
的值是 ; ,若
,若 ,则
,则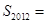 .
. ,
,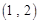 ,
, ,
, ,
,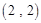 ,
, ,
, ,
, ,
,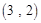 ,
, ,……,则第
,……,则第 个数对是( )
个数对是( )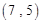




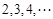 堆最底层(第一层)分别按图1所示方式固定摆放,从第二层开始,每层的小球自然垒放在下一层之上,第
堆最底层(第一层)分别按图1所示方式固定摆放,从第二层开始,每层的小球自然垒放在下一层之上,第 堆第
堆第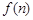 表示第
表示第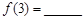 ;
; (
( 的答案用
的答案用 中,
中, ,
, ,则数列通项
,则数列通项 __________
__________ 的一个通项公式是
的一个通项公式是


