题目内容
【题目】定义在[﹣1，1]上的奇函数f（x）满足当﹣1≤x＜0时，f（x）=
.
（1）求f（x）在[﹣1，1]上的解析式；
（2）当x∈（0，1]时，函数g（x）=
﹣m有零点，试求实数m的取值范围．
【答案】（1）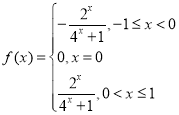
；（2）（1，13].
【解析】
试题（1）可知f（0）=0，再设0＜x≤1，则﹣1≤﹣x＜0，从而得到f（x）=﹣f（﹣x）=﹣（﹣ 
）= 
，从而解得；（2）可化为m=4x+1﹣2x=（2x﹣ 
）2+ 
，从而求实数m的取值范围．
试题解析：
（1）∵f（x）在[﹣1，1]上的奇函数， ∴f（0）=0，
设0＜x≤1，则﹣1≤﹣x＜0，
故f（x）=﹣f（﹣x）=﹣（﹣ 
）= 
，
故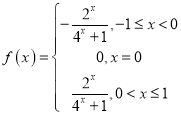
；
（2）当x∈（0，1]时，函数g（x）= 
﹣m=4x+1﹣2x﹣m，
故m=4x+1﹣2x=（2x﹣ 
）2+ 
，
∵x∈（0，1]，∴2x∈（1，2]，
∴1＜4x+1﹣2x≤13，
故实数m的取值范围为（1，13]
练习册系列答案
53天天练系列答案
相关题目
