题目内容
10、设a、b是两个非零向量,则“(a+b)2=|a|2+|b|2”是“a⊥b”的( )
分析:设a、b是两个非零向量,“(a+b)2=|a|2+|b|2”?a•b=0,即a⊥b;a⊥b?a•b=0即(a+b)2=|a|2+|b|2?结论.
解答:解:设a、b是两个非零向量,“(a+b)2=|a|2+|b|2”?(a+b)2=|a|2+|b|2+2ab=|a|2+|b|2?a•b=0,即a⊥b;
a⊥b?a•b=0即(a+b)2=|a|2+|b|2所以“(a+b)2=|a|2+|b|2”是“a⊥b”的充要条件.
故选C.
a⊥b?a•b=0即(a+b)2=|a|2+|b|2所以“(a+b)2=|a|2+|b|2”是“a⊥b”的充要条件.
故选C.
点评:充要条件是高考必考内容;本题还考查平面向量数量积的运算,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,
, 是两个非零向量,则“向量
是两个非零向量,则“向量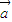 ,
,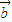 是两个非零向量,则“向量
是两个非零向量,则“向量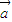 ,
,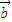 的夹角为锐角”是“函数f(x)=(x
的夹角为锐角”是“函数f(x)=(x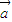 +
+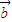 )•(
)•(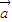 -x
-x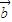 )的图象是一条开口向下的抛物线”的( )
)的图象是一条开口向下的抛物线”的( )