题目内容
已知函数f(x)=px- -2lnx。
-2lnx。
(1)若p=2,求曲线f(x)在点(1,f(1))处的切线;
(2)若函数f(x)在其定义域内为增函数,求正实数p的取值范围;
(3)设函数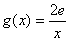 ,若在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立,求实数p的取值范围。
,若在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立,求实数p的取值范围。
 -2lnx。
-2lnx。(1)若p=2,求曲线f(x)在点(1,f(1))处的切线;
(2)若函数f(x)在其定义域内为增函数,求正实数p的取值范围;
(3)设函数
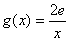 ,若在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立,求实数p的取值范围。
,若在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立,求实数p的取值范围。解:(1)当p=2时,函数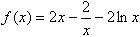
f(1)=2-2-2ln1=0,f'(x)=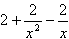
曲线f(x)在点(1,f(1))处的切线的斜率为f'(1)=2+2-2=2
从而曲线f(x)在点(1,f(1))处的切线方程为y-0=2(x-1),
即y=2x-2。
(2)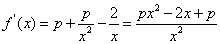
令h(x)=px2-2x+p,要使f(x)在定义域(0,+∞)内是增函数,
只需h(x)≥0在(0,+∞)内恒成立,
由题意p>0,h(x)=px2-2x+p的图象为开口向上的抛物线,对称轴方程为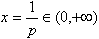
∴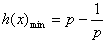
只需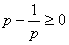
即p≥1时,h(x)≥0,f'(x)≥0,
∴f(x)在(0,+∞)内为增函数,正实数p的取值范围是[1,+∞)。
(3)∵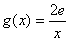 在[1,e]上是减函数,
在[1,e]上是减函数,
∴x=e时,g(x)min=2
x=1时,g(x)max=2e,
即g(x)∈[2,2e]
①当p<0时,h(x)=px2-2x+p其图象为开口向下的抛物线,对称轴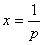 在y轴的左侧,
在y轴的左侧,
且h(0)<0,
所以f(x)在x∈ [1,e]内是减函数,
当p=0时,h(x)=-2x
因为x∈[1,e],
所以h(x)<0,
此时,f(x)在x∈[1,e]内是减函数,
故当p≤0时,f(x)在x∈[1,e]上单调递减 =f(1)=0<2,不合题意;
=f(1)=0<2,不合题意;
②当0<p<1时,x∈[1,e]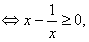
所以f(x)=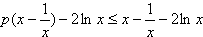
又由(2)知当p=1时f(x)在 x∈[1,e]上是增函数,
∴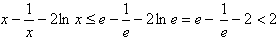
不合题意;
③当p≥1时,由(2)知f(x)在x∈[1,e]上是增函数
f(1)= 0<2
又g(x)在x∈[1,e]上是减函数,
故只需f(x)max>g(x)min,x∈[1,e],
而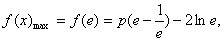
g(x)min=2,即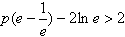
解得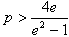
所以实数p的取值范围是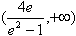 。
。
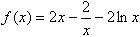
f(1)=2-2-2ln1=0,f'(x)=
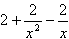
曲线f(x)在点(1,f(1))处的切线的斜率为f'(1)=2+2-2=2
从而曲线f(x)在点(1,f(1))处的切线方程为y-0=2(x-1),
即y=2x-2。
(2)
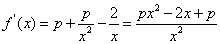
令h(x)=px2-2x+p,要使f(x)在定义域(0,+∞)内是增函数,
只需h(x)≥0在(0,+∞)内恒成立,
由题意p>0,h(x)=px2-2x+p的图象为开口向上的抛物线,对称轴方程为
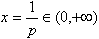
∴
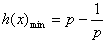
只需
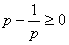
即p≥1时,h(x)≥0,f'(x)≥0,
∴f(x)在(0,+∞)内为增函数,正实数p的取值范围是[1,+∞)。
(3)∵
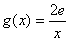 在[1,e]上是减函数,
在[1,e]上是减函数, ∴x=e时,g(x)min=2
x=1时,g(x)max=2e,
即g(x)∈[2,2e]
①当p<0时,h(x)=px2-2x+p其图象为开口向下的抛物线,对称轴
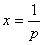 在y轴的左侧,
在y轴的左侧,且h(0)<0,
所以f(x)在x∈ [1,e]内是减函数,
当p=0时,h(x)=-2x
因为x∈[1,e],
所以h(x)<0,

此时,f(x)在x∈[1,e]内是减函数,
故当p≤0时,f(x)在x∈[1,e]上单调递减
 =f(1)=0<2,不合题意;
=f(1)=0<2,不合题意; ②当0<p<1时,x∈[1,e]
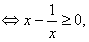
所以f(x)=
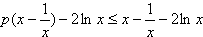
又由(2)知当p=1时f(x)在 x∈[1,e]上是增函数,
∴
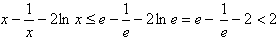
不合题意;
③当p≥1时,由(2)知f(x)在x∈[1,e]上是增函数
f(1)= 0<2
又g(x)在x∈[1,e]上是减函数,
故只需f(x)max>g(x)min,x∈[1,e],
而
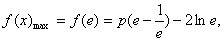
g(x)min=2,即
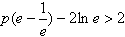
解得
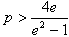
所以实数p的取值范围是
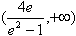 。
。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目