题目内容
【题目】设定义在D上的函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,当
,当![]() 时,若
时,若![]() 在D内恒成立,则称P点为函数
在D内恒成立,则称P点为函数![]() 的“类对称中心点”,则函数
的“类对称中心点”,则函数![]() 的“类对称中心点”的坐标是________.
的“类对称中心点”的坐标是________.
【答案】![]()
【解析】
由求导公式求出函数f(x)的导数,由导数的几何意义和条件求出切线方程,再求出y=g(x),设F(x)=f(x)﹣g(x),求出导数化简后利用分类讨论和导数与函数单调性的关系,判断出F(x)的单调性和最值,从而可判断出![]() 的符号,再由“类对称中心点”的定义确定“类对称中心点”的坐标.
的符号,再由“类对称中心点”的定义确定“类对称中心点”的坐标.
解:由题意得,f′(x)![]() ,f(x0)
,f(x0)![]() (x>0),
(x>0),
即函数y=f(x)的定义域D=(0,+∞),
所以函数y=f(x)在点P(x0,f(x0))处的切线方程l方程为:
y﹣(![]() )=(
)=(![]() )(x﹣x0),
)(x﹣x0),
则g(x)=(![]() )(x﹣x0)+(
)(x﹣x0)+(![]() ),
),
设F(x)=f(x)﹣g(x)![]() lnx﹣[(
lnx﹣[(![]() )(x﹣x0)+(
)(x﹣x0)+(![]() )],
)],
则F(x0)=0,
所以F′(x)=f′x)﹣g′(x)![]() (
(![]() )
)![]()
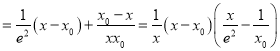
当0<x0<e时,F(x)在(x0,![]() )上递减,
)上递减,
∴x∈(x0,![]() )时,F(x)<F(x0)=0,此时
)时,F(x)<F(x0)=0,此时![]() ,
,
当x0>e时,F(x)在(![]() ,x0)上递减;
,x0)上递减;
∴x∈(![]() ,x0)时,F(x)>F(x0)=0,此时
,x0)时,F(x)>F(x0)=0,此时![]() ,
,
∴y=F(x)在(0,e)∪(e,+∞)上不存在“类对称点”.
若x0=e,![]() 0,则F(x)在(0,+∞)上是增函数,
0,则F(x)在(0,+∞)上是增函数,
当x>x0时,F(x)>F(x0)=0,当x<x0时,F(x)<F(x0)=0,
故![]() ,
,
即此时点P是y=f(x)的“类对称点”,
综上可得,y=F(x)存在“类对称点”,e是一个“类对称点”的横坐标,
又f(e)![]() ,所以函数f(x)的“类对称中心点”的坐标是
,所以函数f(x)的“类对称中心点”的坐标是![]() ,
,
故答案为:![]() .
.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目