题目内容
(2011•洛阳一模)已知m=
lnxdx,n=
|log
x|dx,则m,n的关系是( )
| ∫ | 2 1 |
| ∫ | 2 1 |
| 1 |
| 2 |
分析:根据定积分的几何意义,分别讨论函数y=lnx及函数y=|log
x|的图象在x轴上方的情况,然后由微积分基本定理分析二个定积分对应曲边梯形的面积的大小即可.
| 1 |
| 2 |
解答: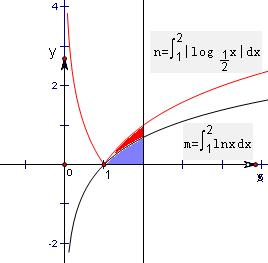 解:m=
解:m=
lnxdx的几何意义表示函数y=lnx的图象在x∈[1,2]时与x轴围成的图形的面积,
n=
|log
x|dx表示函数y=|log
x|的图象在x∈[1,2]时与x轴围成的图形的面积,如图,
观察图形可得m<n
故选A.
 解:m=
解:m=| ∫ | 2 1 |
n=
| ∫ | 2 1 |
| 1 |
| 2 |
| 1 |
| 2 |
观察图形可得m<n
故选A.
点评:本题考查了不等关系与不等式,考查了利用微积分基本定理求定积分,解答此题的关键是对定积分的几何意义的理解与掌握,此题是中档题.

练习册系列答案
相关题目
 (2011•洛阳一模)如图,是一个几何体的三视图,侧视图和正视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的侧面积( )
(2011•洛阳一模)如图,是一个几何体的三视图,侧视图和正视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的侧面积( )