Question

【题目】已知函数f（x）= ．
（1）求f（f（ ））；
（2）若x0满足f（f（x0））=x0 ， 且f（x0）≠x0 ， 则称x0为f（x）的二阶不动点，求函数f（x）的二阶不动点的个数．

Answer 1

【答案】
（1）解：∵f（x）= ．

∴f（ ））=ln = ，

∴f（f（ ））=f（ ）=2﹣2× =1

（2）解：函数f（x）= ．x∈[0， ），f（x）=2﹣2x∈（1，2]，

x∈[ ，1），f（x）=2﹣2x∈（0，1]，

x∈[1，e]，f（x）=lnx∈（0，1），

∴f（f（x））= ，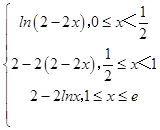

若x0满足f（f（x0））=x0，且f（x0）≠x0，则称x0为f（x）的二阶不动点，

所以：x0∈[0， ），ln（2﹣2x0）=x0，由y=ln（2﹣x0），y=x0，图象可知：

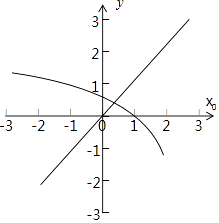
存在满足题意的不动点．

x0∈[ ，1），﹣2+4x0=x0，解得x0= ，满足题意．

x0∈[1，e]，2﹣2lnx0=x0，即2﹣x0=2lnx0，由y=2﹣x0，y=2lnx0，图象可知：

存在满足题意的不动点．

函数f（x）的二阶不动点的个数为：3个

【解析】（1）利用分段函数，逐步求解函数值即可．（2）利用分段函数求出f（f（x0））的解析式，然后通过求解方程得到函数f（x）的二阶不动点的个数．