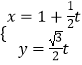题目内容
【题目】已知△ABC的内角A,B,C的对边分别为a,b,c,且ctanC= ![]() (acosB+bcosA).
(acosB+bcosA).
(1)求角C;
(2)若c=2 ![]() ,求△ABC面积的最大值.
,求△ABC面积的最大值.
【答案】
(1)解:ctanC= ![]() (acosB+bcosA),
(acosB+bcosA),
由正弦定理可得:sinCtanC= ![]() (sinAcosB+sinBcosA)=
(sinAcosB+sinBcosA)= ![]() sin(A+B)=
sin(A+B)= ![]() sinC.
sinC.
∴tanC= ![]() ,C∈(0,π).
,C∈(0,π).
∴C= ![]() .
.
(2)解:由余弦定理可得:12=c2=a2+b2﹣2abcosC≥2ab﹣ab=ab,
可得ab≤12,当且仅当a=2 ![]() 时取等号.
时取等号.
∴△ABC面积的最大值= ![]() =3
=3 ![]() .
.
【解析】(1)利用正弦定理与和差公式即可得出.(2)利用余弦定理、基本不等式的性质、三角形面积计算公式即可得出.
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识,掌握正弦定理:![]() ,以及对余弦定理的定义的理解,了解余弦定理:
,以及对余弦定理的定义的理解,了解余弦定理:![]() ;
;![]() ;
;![]() .
.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
【题目】某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示.
成绩分组 | 频数 | 频率 |
(160,165] | 5 | 0.05 |
(165,170] | ① | 0.35 |
(170,175] | 30 | ② |
(175,180] | 20 | 0.20 |
(180,185] | 10 | 0.10 |
合计 | 100 | 1 |
(1)请先求出频率分布表中①、②位置相应的数据,再画出频率分布直方图;
(2)为了能选拔出最优秀的学生,该高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官的面试,求第四组至少有一名学生被考官A面试的概率?