题目内容
【题目】在平面直角坐标系xOy中,直线l的参数方程为 ![]() (t为参数,0≤α<π),以坐标原点O为极点,x轴的正半轴为极轴,并取相同的长度单位,建立极坐标系.曲线C1:p=1.
(t为参数,0≤α<π),以坐标原点O为极点,x轴的正半轴为极轴,并取相同的长度单位,建立极坐标系.曲线C1:p=1.
(1)若直线l与曲线C1相交于点A,B,点M(1,1),证明:|MA||MB|为定值;
(2)将曲线C1上的任意点(x,y)作伸缩变换 ![]() 后,得到曲线C2上的点(x',y'),求曲线C2的内接矩形ABCD周长的最大值.
后,得到曲线C2上的点(x',y'),求曲线C2的内接矩形ABCD周长的最大值.
【答案】
(1)证明:∵曲线C1:p=1,∴曲线C1:x2+y2=1.
联立 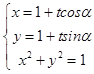 ,得t2+2t(cosα+sinα)+1=0,
,得t2+2t(cosα+sinα)+1=0,
∴|MA||MB|=|t1t2|=1.
(2)解:将曲线C1上的任意点(x,y)作伸缩变换 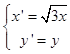 ,
,
伸缩变换后得C2: ![]() .
.
其参数方程为:  .
.
不妨设点A(m,n)在第一象限,
由对称性知:周长为 ![]() =
= ![]() ,(
,( ![]() 时取等号),
时取等号),
∴曲线C2的内接矩形ABCD周长的最大值为8.
【解析】(1)求出曲线C1:x2+y2=1.直线l的参数方程代入,得t2+2t(cosα+sinα)+1=0,由此能证明|MA||MB|为定值.(2)将曲线C1上的任意点(x,y)伸缩变换后得C2: ![]() .由此能求出曲线C2的内接矩形ABCD周长的最大值.
.由此能求出曲线C2的内接矩形ABCD周长的最大值.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目