题目内容
高二年级举行一次演讲赛共有10位同学参赛，其中一班有3位，二班有2位，其它班有5位，若采用抽签的方式确定他们的演讲顺序，则一班有3位同学恰好被排在一起（指演讲序号相连），而二班的2位同学没有被排在一起的概率为：（ ）
A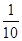． | B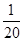． | C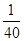． | D． |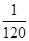
B
将一班3位同学捆绑在一起与其他班5位同学一起排列，有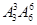
种排法。再将二班2位同学插入到8位排好的同学的7个空隙中，有
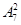种排法。所以总共有
种排法，其概率为
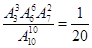，故选B
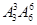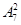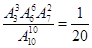种排法。再将二班2位同学插入到8位排好的同学的7个空隙中，有种排法。所以总共有种排法，其概率为，故选B
练习册系列答案
相关题目
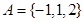中随机选取一个数记为
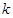，从集合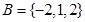
中随机选取一个数记为
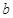，则直线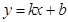
不经过第三象限的概率为 ( ▲ )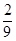
.
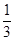
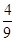
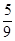
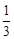
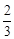
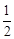
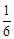
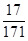
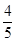，则小组中女生人数为 ．