题目内容
一个口袋内装有大小相等的2个白球和3个黑球,从中摸出2个球,则摸到2个黑球的概率为
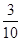
分析:把白球编号为1,2,黑球记为a,b,c,用列举法求得共有10种摸法.由于其中摸出两个黑球的方法有3种,由此可得摸出2个黑球的概率.
解答:解:白球编号为1,2,黑球记为a,b,c,
共有10种摸法:(1,2),(1,a),(1,b),(1,c),(2,a),(2,b),(2,c),
(a,b),(a,c),(b,c).--(4分)
其中,摸出两个黑球的方法有 (a,b),(a,c),(b,c)3种,
故摸出2个黑球的概率为 p=
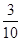 .
.点评:本题考查古典概型问题,可以列举出试验发生包含的事件和满足条件的事件,应用列举法来解题是这一部分的最主
要思想,属于基础题.

练习册系列答案
相关题目
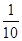
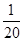
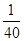
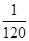




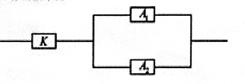
 的概率;
的概率; ,测得相关指数
,测得相关指数 ;乙给出的拟合曲线的方程是:
;乙给出的拟合曲线的方程是: ,测得相关指数
,测得相关指数 。请判断用哪一个方程拟合效果会更好,并用较好的曲线方程估计x=10时y的值。
。请判断用哪一个方程拟合效果会更好,并用较好的曲线方程估计x=10时y的值。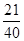
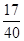
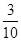
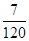



 孩,把她们分别记为A,C,J,K,S。她们应聘秘书工作,但只有3个秘书职位,因此5人中仅有三人被录用。如果5人被录用的机会
孩,把她们分别记为A,C,J,K,S。她们应聘秘书工作,但只有3个秘书职位,因此5人中仅有三人被录用。如果5人被录用的机会