Question

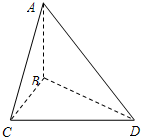（2013•嘉定区二模）（理）如图：已知AB⊥平面BCD，BC⊥CD，AD与平面BCD所成的角为30°，且AB=BC=2．
（1）求AD与平面ABC所成角的大小；
（2）求点B到平面ACD的距离．

Answer 1

分析：（1）由AB⊥平面BCD，所以AB⊥CD，又BC⊥CD，所以CD⊥平面ABC，∠DAC就是AD与平面ABC所成的角，然后直接解直角三角形即可；
（2）设出点B到平面ACD的距离，直接利用等积法求距离．

解答：解：（1）如图，

因为AB⊥平面BCD，所以AB⊥CD，又BC⊥CD，所以CD⊥平面ABC，∠DAC就是AD与平面ABC所成的角．
因为AB⊥平面BCD，AD与平面BCD所成的角为30°，故∠ADB=30°，
由AB=BC=2，得AD=4，AC=2

2

，
所以cos∠DAC=

AC

AD

=

2

2

，
所以AD与平面ABC所成角的大小为45°；
（2）设点B到平面ACD的距离为d，由（1）可得BD=2

3

，CD=2

2

，
则VA-BCD=

1

3

S△BCD•AB=

1

6

BC•CD•AB
=

1

6

×2×2

2

×2=

4 2

3

．
VB-ACD=

1

3

S△ACD•d=

1

6

AC•CD•d
=

1

6

×2

2

×2

2

d=

4

3

d．
由V_A-BCD=V_B-ACD，得

4 2

3

=

4

3

d，所以d=

2

．
所以点B到平面ACD的距离为

2

．

点评：本题考查了直线和平面所成角的计算，考查了利用等积法求点到面的距离，变换椎体的顶点，利用其体积相等求空间中点到面的距离是较有效的方法，此题是中档题．