题目内容
(本题10分)
已知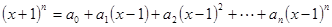 (
(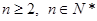 ),
),
(1)当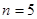 时,求
时,求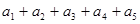 的值;
的值;
(2)设 ,试用数学归纳法证明:
,试用数学归纳法证明:
当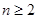 时,
时, 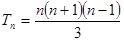 。
。
已知
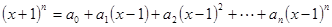 (
(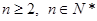 ),
),(1)当
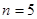 时,求
时,求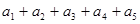 的值;
的值;(2)设
 ,试用数学归纳法证明:
,试用数学归纳法证明:当
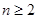 时,
时, 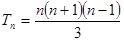 。
。(1)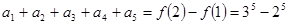 ; (2)见解析;
; (2)见解析;
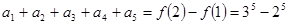 ; (2)见解析;
; (2)见解析;本试题主要是考查了二项式定理和数学归纳法的运用。
(1)记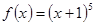 ,
,
则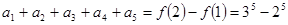
(2)设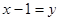 ,则原展开式变为:
,则原展开式变为: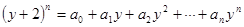 ,
,
则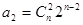
所以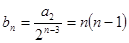
然后求和,并运用数学归纳法证明。
解:(1)记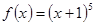 ,
,
则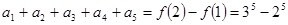 (4分)
(4分)
(2)设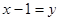 ,则原展开式变为:
,则原展开式变为: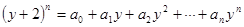 ,
,
则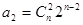
所以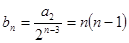 (6分)
(6分)
当 时,
时,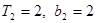 ,结论成立
,结论成立
假设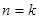 时成立,即
时成立,即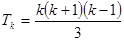
那么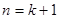 时,
时,
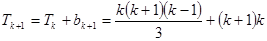

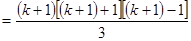 ,结论成立。(9分)
,结论成立。(9分)
所以当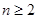 时,
时,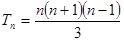 。(10分)
。(10分)
(1)记
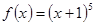 ,
,则
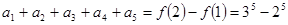
(2)设
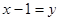 ,则原展开式变为:
,则原展开式变为: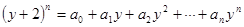 ,
,则
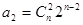
所以
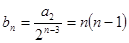
然后求和,并运用数学归纳法证明。
解:(1)记
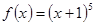 ,
,则
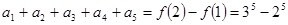 (4分)
(4分)(2)设
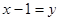 ,则原展开式变为:
,则原展开式变为: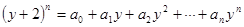 ,
,则
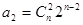
所以
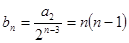 (6分)
(6分)当
 时,
时,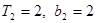 ,结论成立
,结论成立假设
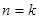 时成立,即
时成立,即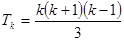
那么
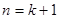 时,
时,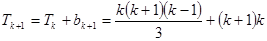

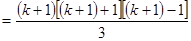 ,结论成立。(9分)
,结论成立。(9分)所以当
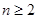 时,
时,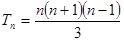 。(10分)
。(10分)
练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
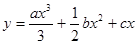 在点
在点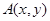 处的切线斜率为
处的切线斜率为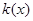 ,且
,且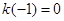 .对一切实数
.对一切实数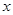 ,不等式
,不等式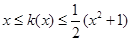 恒成立(
恒成立(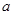 ≠0).
≠0).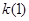 的值;
的值;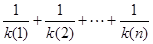 >
>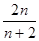 .
.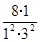 ,
,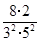 ,…,
,…,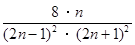 ,….S
,….S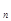 为其前n项和,求S
为其前n项和,求S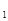 、S
、S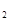 、S
、S 、S
、S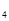 ,推测S
,推测S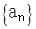 的前n项和为
的前n项和为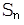 且方程
且方程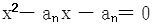 有一根为
有一根为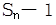 ,n=1,2,3…,试求
,n=1,2,3…,试求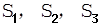 的值,猜想
的值,猜想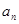 }满足
}满足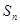 +
+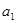 ,
,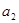 ,
,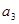 的值;
的值; 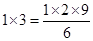 ;
;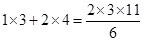 ;
;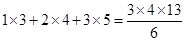 ,
,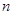 堆的第
堆的第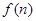 表示第
表示第


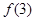 ;
;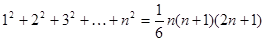 )
)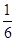 n(n+1)(2n+1)(n∈N*)”,当n=k+1时,应在n=k时的等式左边添加的项是________.
n(n+1)(2n+1)(n∈N*)”,当n=k+1时,应在n=k时的等式左边添加的项是________.