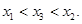题目内容
定义:已知函数f(x)在[m,n](m<n)上的最小值为t,若t≤m恒成立,则称函数f(x)在[m,n](m<n)上具有“DK”性质.已知f(x)=ax2-|x|+2a-1
(1)若a=1,判断函数f(x)在[1,2]上是否具有“DK”性质,说明理由.
(2)若f(x)在[1,2]上具有“DK”性质,求a的取值范围.
(1)若a=1,判断函数f(x)在[1,2]上是否具有“DK”性质,说明理由.
(2)若f(x)在[1,2]上具有“DK”性质,求a的取值范围.
分析:(1)求出断函数f(x)在[1,2]上的最小值,利用定义,可以判断;
(2)对a进行讨论,确定函数在[1,2]上的单调性,求出最小值,即可求得结论.
(2)对a进行讨论,确定函数在[1,2]上的单调性,求出最小值,即可求得结论.
解答:解:(1)∵a=1,x∈[1,2]
∴f(x)=x2-|x|+1=x2-x+1
,
∴f(x)min=1≤1,
∴函数f(x)在[1,2]上具有“DK”性质.…(4分)
(2)当x∈[1,2]时,f(x)=ax2-x+2a-1…(5分)
①若a=0,则f(x)=-x-1在区间[1,2]上是减函数,f(x)min=f(2)=-3≤1
满足函数f(x)具有“DK”性质,∴a=0…(6分)
②若a≠0,则f(x)=a(x-
)2+2a-
-1,函数的对称轴为直线x=
当a<0时,f(x)在区间[1,2]上是减函数,f(x)min=f(2)=6a-3≤1
满足函数f(x)具有“DK”性质,∴a<0…(7分)
当0<
<1,即a>
时,f(x)在区间[1,2]上是增函数f(x)min=f(1)=3a-2,
若函数f(x)具有“DK”性质,则3a-2≤1
∴
<a≤1…(8分)
当1≤
≤2,即
≤a≤
时,f(x)min=f(
)=2a-
-1
若函数f(x)具有“DK”性质,则2a-
-1≤1得
≤a≤
∴
≤a≤
…(9分)
当
>2,即0<a<
时,f(x)在区间[1,2]上是减函数,f(x)min=f(2)=6a-3≤1,满足函数f(x)具有“DK”性质,∴0<a<
…(10分)
综上所述,若f(x)在[1,2]上具有“DK”性质,则a的取值范围为(-∞,1].…(12分)
∴f(x)=x2-|x|+1=x2-x+1
|
∴f(x)min=1≤1,
∴函数f(x)在[1,2]上具有“DK”性质.…(4分)
(2)当x∈[1,2]时,f(x)=ax2-x+2a-1…(5分)
①若a=0,则f(x)=-x-1在区间[1,2]上是减函数,f(x)min=f(2)=-3≤1
满足函数f(x)具有“DK”性质,∴a=0…(6分)
②若a≠0,则f(x)=a(x-
| 1 |
| 2a |
| 1 |
| 4a |
| 1 |
| 2a |
当a<0时,f(x)在区间[1,2]上是减函数,f(x)min=f(2)=6a-3≤1
满足函数f(x)具有“DK”性质,∴a<0…(7分)
当0<
| 1 |
| 2a |
| 1 |
| 2 |
若函数f(x)具有“DK”性质,则3a-2≤1
∴
| 1 |
| 2 |
当1≤
| 1 |
| 2a |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2a |
| 1 |
| 4a |
若函数f(x)具有“DK”性质,则2a-
| 1 |
| 4a |
2-
| ||
| 4 |
2+
| ||
| 4 |
∴
| 1 |
| 4 |
| 1 |
| 2 |
当
| 1 |
| 2a |
| 1 |
| 4 |
| 1 |
| 4 |
综上所述,若f(x)在[1,2]上具有“DK”性质,则a的取值范围为(-∞,1].…(12分)
点评:本题考查新定义,考查函数的最值,考查分类讨论的数学思想,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
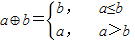 已知函数f(x)=x2⊕x,求f(2)= .
已知函数f(x)=x2⊕x,求f(2)= .
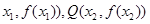 是函数 f(x)图象上任意两点,且0<x1<x2,若存在实数x3>0,使得
是函数 f(x)图象上任意两点,且0<x1<x2,若存在实数x3>0,使得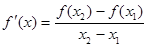 .请结合(I)中的结论证明:
.请结合(I)中的结论证明: