Question

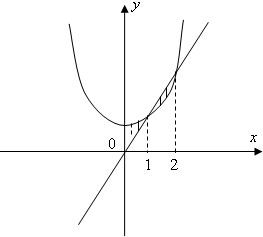
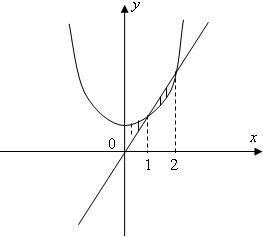
由曲线y=x²+2与直线y=3x，x=0，x=2所围成平面图形的面积为

 

．

Answer 1

分析：先求出曲线与直线的交点，设围成的平面图形面积为A，利用定积分求出A即可．

解答：解：联立曲线与直线得

y=x2+2 y=3x

，
解得

x=1 y=3

或

x=2 y=6

设曲线y=x²+2与直线y=3x，x=0，x=2所围成的平面图形的面积为A
则A=∫₀¹[（x²+2）-3x]dx+∫₁²[3x-（x²+2）]dx=1
故答案为1．

点评：考查学生利用定积分求平面图形面积的能力，考查运算能力，基础题．