Question

【题目】已知双曲线C：－＝1(a>0，b>0)与椭圆＋＝1的焦点重合，离心率互为倒数，设F1、F2分别为双曲线C的左、右焦点，P为右支上任意一点，则的最小值为________．

Answer 1

【答案】8

【解析】

求出椭圆的离心率和焦点，从而得双曲线的离心率，双曲线的实半轴长，可得，由双曲线的定义得PF1＝PF2＋2，这样就可表示为的函数，于是可利用基本不等式求得最小值

设椭圆的长半轴长为a1，短半轴长为b1，半焦距为c，

则c＝＝＝2，

故椭圆的离心率e1＝＝，

从而双曲线的离心率，可得a＝1，

根据双曲线的定义有PF1－PF2＝2a，即PF1＝PF2＋2，

故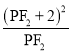＝＝＝PF2＋＋4，

由双曲线的范围可得PF2≥c－a＝1，

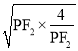根据基本不等式可得PF2＋＋4≥2＋4＝8，

当且仅当PF2＝，

即PF2＝2时取“＝”，

所以的最小值为8.

故答案为：8．