题目内容
已知非零实数a1，a2，b1，b2，若条件p：“
=
”，条件q“关于x的不等式a1x+b1＞0与a2x+b2＞0的解集相同”．则条件p是q的（ ）
| a1 |
| b1 |
| a2 |
| b2 |
分析：由“
=
”不能推出“关于x的不等式a1x+b1＞0与a2x+b2＞0的解集相同”，“关于x的不等式a1x+b1＞0与a2x+b2＞0的解集相同”⇒“
=
”，从而能够得到正确答案．
| a1 |
| b1 |
| a2 |
| b2 |
| a1 |
| b1 |
| a2 |
| b2 |
解答：解：∵若
=
时，如取a1=b1=1，a2=b2=-1，
关于x的不等式a1x+b1＞0与a2x+b2＞0即不等式x+1＞0与-x-1＞0的解集不相同，
∴“
=
”不能推出“关于x的不等式a1x+b1＞0与a2x+b2＞0的解集相同”，
反之，“关于x的不等式a1x+b1＞0与a2x+b2＞0的解集相同”⇒“
=
”，
∴“
=
”是“关于x的不等式a1x+b1＞0与a2x+b2＞0的解集相同”的必要非充分条件．
故选D．
| a1 |
| b1 |
| a2 |
| b2 |
关于x的不等式a1x+b1＞0与a2x+b2＞0即不等式x+1＞0与-x-1＞0的解集不相同，
∴“
| a1 |
| b1 |
| a2 |
| b2 |
反之，“关于x的不等式a1x+b1＞0与a2x+b2＞0的解集相同”⇒“
| a1 |
| b1 |
| a2 |
| b2 |
∴“
| a1 |
| b1 |
| a2 |
| b2 |
故选D．
点评：本题考查必要条件、充分条件和充要条件的性质和应用及一元一次不等式，属于基础题．
练习册系列答案
相关题目
已知a1，a2，b1，b2均为非零实数，集合A={x|a1x+b1＞0}，B={x|a2x+b2＞0}，则“
=
”是“A=B”的（ ）
| a1 |
| a2 |
| b1 |
| b2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
=
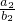”，条件q“关于x的不等式a1x+b1＞0与a2x+b2＞0的解集相同”．则条件p是q的
=
”，条件q“关于x的不等式a1x+b1＞0与a2x+b2＞0的解集相同”．则条件p是q的（ ）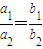
”是“A=B”的（ ）