题目内容
已知a1,a2,b1,b2均为非零实数,集合A={x|a1x+b1>0},B={x|a2x+b2>0},则“
=
”是“A=B”的( )
| a1 |
| a2 |
| b1 |
| b2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
分析:先根据
=
,进行赋值说明此时A≠B,然后根据“M?N,M是N的充分不必要条件,N是M的必要不充分条件”,进行判定即可.
| a1 |
| a2 |
| b1 |
| b2 |
解答:解:∵
=
∴取a1=1,a2=-1,b1=-1,b2=1,A≠B
而A=B?
=
∴“
=
”是“A=B”的必要不充分条件
故选B
| a1 |
| a2 |
| b1 |
| b2 |
∴取a1=1,a2=-1,b1=-1,b2=1,A≠B
而A=B?
| a1 |
| a2 |
| b1 |
| b2 |
∴“
| a1 |
| a2 |
| b1 |
| b2 |
故选B
点评:本题主要考查了以不等式为载体考查两集合相等的充要条件,以及赋值法的运用,属于基础题.

练习册系列答案
相关题目
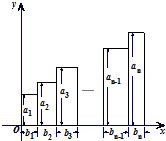 13、已知a1,a2,…,an;b1,b2,…,bn(n是正整数),令L1=b1+b2+…+bn,L2=b2+b3+…+bn,…,Ln=bn、某人用右图分析得到恒等式:a1b1+a2b2+…+anbn=a1L1+c2L2+c3L3+…+ckLk+…+…+cnLn,则ck=
13、已知a1,a2,…,an;b1,b2,…,bn(n是正整数),令L1=b1+b2+…+bn,L2=b2+b3+…+bn,…,Ln=bn、某人用右图分析得到恒等式:a1b1+a2b2+…+anbn=a1L1+c2L2+c3L3+…+ckLk+…+…+cnLn,则ck=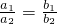 ”是“A=B”的
”是“A=B”的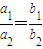 ”是“A=B”的( )
”是“A=B”的( )