Question

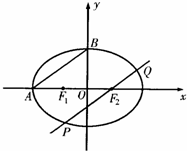如图所示，F₁、F₂分别为椭圆C：

x2

a2

+

y2

b2

=1 (a＞b＞0)的左、右两个焦点，A、B为两个顶点，已知椭圆C上的点(1，

3

2

)到F₁、F₂两点的距离之和为4．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过椭圆C的焦点F₂作AB的平行线交椭圆于P、Q两点，求△F₁PQ的面积．

Answer 1

分析：（Ⅰ）由题设知：2a=4，即a=2，将点(1，

3

2

)代入椭圆方程得 

1

22

+

( 3 2 )2

b2

=1，解得b²=3，由此能得到椭圆方程．
（Ⅱ）由A(-2，0)， B(0，

3

)，知kPQ=kAB=

3

2

，所以PQ所在直线方程为y=

3

2

(x-1)，由

y= 3 2 (x-1) x2 4 + y2 3 =1

得 8y2+4

3

y-9=0，设P （x₁，y₁），Q （x₂，y₂），由韦达定理能导出|y1-y2|=

(y1+y2)2-4y1y2

=

3 4 +4× 9 8

=

21

2

，由此能求出△F₁PQ的面积．

解答：解：（Ⅰ）由题设知：2a=4，即a=2
将点(1，

3

2

)代入椭圆方程得 

1

22

+

( 3 2 )2

b2

=1，解得b²=3
∴c²=a²-b²=4-3=1，故椭圆方程为

x2

4

+

y2

3

=1--------------（3分）
（Ⅱ）由（Ⅰ）知A(-2，0)， B(0，

3

)，∴kPQ=kAB=

3

2

，
∴PQ所在直线方程为y=

3

2

(x-1)---------------（5分）
由

y= 3 2 (x-1) x2 4 + y2 3 =1

得 8y2+4

3

y-9=0---------------------------------（7分）
设P （x₁，y₁），Q （x₂，y₂），则y1+y2=-

3

2

， y1•y2=-

9

8

--------（8分）
∴|y1-y2|=

(y1+y2)2-4y1y2

=

3 4 +4× 9 8

=

21

2

--------------------------（9分）
∴S△F1PQ=

1

2

|F1F2|•|y1-y2|=

1

2

×2×

21

2

=

21

2

．-------------------------（10分）

点评：本题考查椭圆C的方程和求△F₁PQ的面积．解题时要认真审题，注意挖掘题设中的隐含条件，合理地进行等价转化．