题目内容
 如图所示,F1、F2分别为椭圆C:
如图所示,F1、F2分别为椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
(1)求椭圆C的方程;
(2)证明:椭圆C上任意一点M(x0,y0)到右焦点F2的距离的最小值为1.
(3)作AB的平行线交椭圆C于P、Q两点,求弦长|PQ|的最大值,并求|PQ|取最大值时△F1PQ的面积.
分析:(1)根据顶点B(0,
)到F1、F2两点的距离之和为4,可得a=2,b=
,从而可求椭圆方程;
(2)计算出椭圆C上任意一点M(x0,y0)到右焦点F2的距离,根据x0∈[-2,2],可证结论;
(3)先求|PQ|max=
,再求点F1(-1,0)到直线PQ的距离,即可求得△F1PQ的面积.
| 3 |
| 3 |
(2)计算出椭圆C上任意一点M(x0,y0)到右焦点F2的距离,根据x0∈[-2,2],可证结论;
(3)先求|PQ|max=
| 14 |
解答:(1)解:由已知得a=2,b=
,
∴椭圆方程为
+
=1…(2分)
(2)证明:∵M(x0,y0),F2(1,0)且x0∈[-2,2],
∴|MF2|=
=
=|
x0-2|∈[1,3]…(4分)
∴仅当M(x0,y0)为右顶点时|MF2|min=1…(5分)
(3)解:设P(x1,y1),Q(x2,y2)∵kAB=
,
∴可设直线PQ:y=
x+m,
代入
+
=1,得3x2+2
mx+2m2-6=0…(7分)
由韦达定理知,x1+x2=-
,x1x2=
,…(9分)
又y1=
x1+m,y2=
x2+m
∴|PQ|=
=
=
=
=
仅当m=0时|PQ|max=
…(12分)
而点F1(-1,0)到直线PQ:
x-2y=0的距离h=
=
,
∴S△F1PQ=
|PQ|•h=
.…(14分)
| 3 |
∴椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)证明:∵M(x0,y0),F2(1,0)且x0∈[-2,2],
∴|MF2|=
| (x0-1)2+(y0-0)2 |
(
|
| 1 |
| 2 |
∴仅当M(x0,y0)为右顶点时|MF2|min=1…(5分)
(3)解:设P(x1,y1),Q(x2,y2)∵kAB=
| ||
| 2 |
∴可设直线PQ:y=
| ||
| 2 |
代入
| x2 |
| 4 |
| y2 |
| 3 |
| 3 |
由韦达定理知,x1+x2=-
2
| ||
| 3 |
| 2m2-6 |
| 3 |
又y1=
| ||
| 2 |
| ||
| 2 |
∴|PQ|=
| (x1-x2)2+(y1-y2)2 |
(1+
|
(1+
|
|
|
仅当m=0时|PQ|max=
| 14 |
而点F1(-1,0)到直线PQ:
| 3 |
|-
| ||
|
| ||
| 7 |
∴S△F1PQ=
| 1 |
| 2 |
| ||
| 2 |
点评:本题以椭圆的性质为载体,考查椭圆的标准方程,考查直线与椭圆的位置关系,解题的关键是将直线与椭圆方程联立,从而利用韦达定理解题.

练习册系列答案
相关题目
 如图所示,F1,F2分别为椭圆C:
如图所示,F1,F2分别为椭圆C: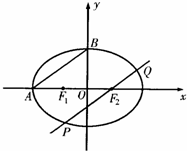 如图所示,F1、F2分别为椭圆C:
如图所示,F1、F2分别为椭圆C: 如图所示,F1、F2分别为椭圆C:
如图所示,F1、F2分别为椭圆C: (2013•牡丹江一模)如图所示,F1和F2分别是双曲线
(2013•牡丹江一模)如图所示,F1和F2分别是双曲线