题目内容
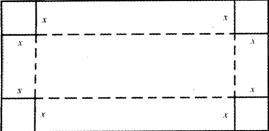
今有一长2米宽1米的矩形铁皮,如图,在四个角上分别截去一个边长为x米的正方形后,沿虚线折起可做成一个无盖的长方体形水箱(接口连接问题不考虑).
(I)求水箱容积的表达式f(x),并指出函数f(x)的定义域;
(II)若要使水箱容积不大于4x3立方米的同时,又使得底面积最大,求x的值.

答案:
解析:
解析:
|
解:(I)由已知该长方体形水箱高为 ∴该水箱容积为 其中正数 ∴所求函数 (II) 答:满足条件的 由 此时的底面积为 由 ∴ |

练习册系列答案
相关题目
 今有一长2米宽1米的矩形铁皮,如图,在四个角上分别截去一个边长为x米的正方形后,沿虚线折起可做成一个无盖的长方体形水箱(接口连接问题不考虑).
今有一长2米宽1米的矩形铁皮,如图,在四个角上分别截去一个边长为x米的正方形后,沿虚线折起可做成一个无盖的长方体形水箱(接口连接问题不考虑).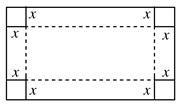
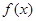 ,并指出函数
,并指出函数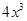 立方米的同时,又使得底面积最大,求x的值.
立方米的同时,又使得底面积最大,求x的值. 今有一长2米宽1米的矩形铁皮,如图,在四个角上分别截去一个边长为x米的正方形后,沿虚线折起可做成一个无盖的长方体形水箱(接口连接问题不考虑).
今有一长2米宽1米的矩形铁皮,如图,在四个角上分别截去一个边长为x米的正方形后,沿虚线折起可做成一个无盖的长方体形水箱(接口连接问题不考虑).