题目内容
已知二次函数y=x2-4x+5,分别求下列条件下函数的值域:
(1)x∈[-1,0];
(2)x∈(1,3);
(3)x∈(4,5].
(1)x∈[-1,0];
(2)x∈(1,3);
(3)x∈(4,5].
分析:先对解析式配方后求出对称轴并画出图象,
(1)由图判断出函数在[-1,0]上递减,再求出最大值和最小值,写出函数的值域即可;
(2)由图判断出函数在(1,3)上单调性,再求出最大值和最小值,写出函数的值域即可;
(3)由图判断出函数在(4,5]上递减,再求出最大值和最小值,写出函数的值域即可.
(1)由图判断出函数在[-1,0]上递减,再求出最大值和最小值,写出函数的值域即可;
(2)由图判断出函数在(1,3)上单调性,再求出最大值和最小值,写出函数的值域即可;
(3)由图判断出函数在(4,5]上递减,再求出最大值和最小值,写出函数的值域即可.
解答:解:由题意得,y=x2-4x+5=(x-2)2+1,关于x=2对称,如图:
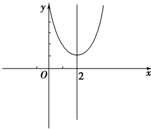
(1)由图得,函数在[-1,0]上递减,
则当x=0时,y=5.当x=-1时,y=10.
即当x∈[-1,0]时,y∈[5,10].
(2)由图得,函数在(1,2]上递减,(2,3)上递增,
则x∈(1,3)时,x=2时,y最小值为1.
当x=1或x=3时,y=2.
又∵x∈(1,3),∴点(1,2),(3,2)为虚点.
∴当x∈(1,3)时,y∈[1,2).
(3)由图得,函数在(4,5]上递增,
当x∈(4,5]时,x=4时,对应值y=5,(4,5)为虚点.
当x=5时,y=10,(5,10)为实点.
∴当x∈(4,5]时,y∈(5,10].

(1)由图得,函数在[-1,0]上递减,
则当x=0时,y=5.当x=-1时,y=10.
即当x∈[-1,0]时,y∈[5,10].
(2)由图得,函数在(1,2]上递减,(2,3)上递增,
则x∈(1,3)时,x=2时,y最小值为1.
当x=1或x=3时,y=2.
又∵x∈(1,3),∴点(1,2),(3,2)为虚点.
∴当x∈(1,3)时,y∈[1,2).
(3)由图得,函数在(4,5]上递增,
当x∈(4,5]时,x=4时,对应值y=5,(4,5)为虚点.
当x=5时,y=10,(5,10)为实点.
∴当x∈(4,5]时,y∈(5,10].
点评:本题考查了二次函数的单调性以及最值的应用,利用配方法化简解析式再画出图象,注意区间的开或闭.

练习册系列答案
相关题目