Question

在数列{a_n}中，，其中θ为方程的解，则这个数列的前n项和S_n为（　　）

A．

B．

C．

D．

Answer 1

考点：

数列的求和；函数的零点．

专题：

综合题；等差数列与等比数列；三角函数的求值．

分析：

由，解得，k∈Z．所以==﹣，故数列{a_n}是首项为，公比为q=的等比数列，由此能求出这个数列的前n项和．

解答：

解：∵，

∴，

∴2sin（2θ﹣）=2，

∴2θ﹣=2kπ+，k∈Z，

解得，k∈Z．

∴

=

==﹣，

∴数列{a_n}是首项为，公比为q=的等比数列，

∴这个数列的前n项和S_n==﹣．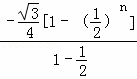

故选A．

点评：

本题考查数列的前n项和的求法，解题时要认真审题，仔细解答，注意三角函数恒等变换的合理运用．