题目内容
一般地,在数列{an}中,如果存在非零常数T,使得am+T=am对任意正整数m均成立,那么就称{an}为周期数列,其中T叫做数列{an}的周期.已知数列{xn}满足xn+1=|xn-xn-1|(n≥2,n∈N*),如果x1=1,x2=a,(a≤1,a≠0),设S2009为其前2009项的和,则当数列{xn}的周期为3时,S2009=
1339+a
1339+a
.分析:首先要弄清题意中所说的周期数列的含义,然后利用这个定义,针对题目中的数列的周期由题意和周期定义知,先求x3,再前三项和s3,最后求s2009.
解答:解:∵xn+1=|xn-xn-1|(n≥2,n∈N*),
且x1=1,x2=a(a≤1,a≠0),
∴x3=|x2-x1|=1-a
∴该数列的前3项的和s3=1+a+(1-a)=2
∵数列{xn}周期为3,
∴该数列的前2009项的和s2009=s2007+x1+x2=
s3+1+a=1339+a,
故答案为1339+a.
且x1=1,x2=a(a≤1,a≠0),
∴x3=|x2-x1|=1-a
∴该数列的前3项的和s3=1+a+(1-a)=2
∵数列{xn}周期为3,
∴该数列的前2009项的和s2009=s2007+x1+x2=
| 2007 |
| 3 |
故答案为1339+a.
点评:本小题主要考查数列具有周期性、数列的前n项和等基础知识,考查运算求解能力,解答关键在于应由题意先求一个周期的和,再求该数列的前n项和sn.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
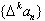 为{an}的k阶差分数列,其中
为{an}的k阶差分数列,其中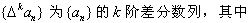
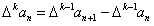 ,且
,且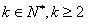 。
。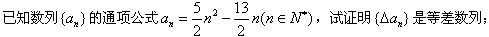
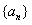 的首项
的首项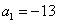 ,且满足
,且满足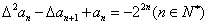 ,求数列
,求数列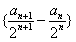 及
及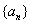 的通项公式;
的通项公式; 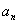 是否存在最小值,若存在求出其最小值,若不存在说明理由。
是否存在最小值,若存在求出其最小值,若不存在说明理由。  n2-
n2- n(n∈N*),试证明{△an}是等差数列;
n(n∈N*),试证明{△an}是等差数列; ,求证:b1+
,求证:b1+ +…+
+…+ <
< .
.