题目内容
设函数f(x)=ax3-2bx2+cx+4d(a、b、c、d∈R)图象关于原点对称,且x=1时,f(x)取极小值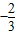 .
.(1)求a、b、c、d的值;
(2)当x∈[-1,1]时,图象上是否存在两点,使得过此两点处的切线互相垂直?试证明你的结论.
【答案】分析:(1)由函数f(x)图象关于原点对称,知对任意实数x有f(-x)=-f(x),由此能求出f(x)的解析式.
(2)由(1)中函数解析式,求出函数的导函数,是否存在x1,x2∈[-1,1],使f'(x1)•f'(x2)═-1,进而得到结论.
解答:解. (1)∵函数f(x)图象关于原点对称,
∴对任意实数x有f(-x)=-f(x),
∴-ax3-2bx2-cx+4d=-ax3+2bx2-cx-4d,
即bx2-2d=0恒成立
∴b=0,d=0,
∴f(x)=ax3+cx,
f'(x)=3ax2+c,
∵x=1时,f(x)取极小值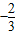 ,
,
∴3a+c=0且a+c=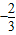 ,
,
解得a= ,c=-1,
,c=-1,
∴f(x)= x3-x.
x3-x.
(2)由(1)得f'(x)=x2-1,
当x∈[-1,1]时,f'(x)∈[-1,0]
当且仅当x=0时,f'(x)=-1
故?x1,x2∈[-1,0]
f'(x1)•f'(x2)≥0恒成立,
即f'(x1)•f'(x2)≠-1恒成立,
故当x∈[-1,1]时,图象上不存在两点,使得过此两点处的切线互相垂直
点评:本题考查的知识点是函数在某点取得极值的条件,利用导数研究函数曲线上某点的切线方程,其中熟练掌握导数法求函数极值和切线斜率的方法是解答的关键.
(2)由(1)中函数解析式,求出函数的导函数,是否存在x1,x2∈[-1,1],使f'(x1)•f'(x2)═-1,进而得到结论.
解答:解. (1)∵函数f(x)图象关于原点对称,
∴对任意实数x有f(-x)=-f(x),
∴-ax3-2bx2-cx+4d=-ax3+2bx2-cx-4d,
即bx2-2d=0恒成立
∴b=0,d=0,
∴f(x)=ax3+cx,
f'(x)=3ax2+c,
∵x=1时,f(x)取极小值
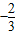 ,
,∴3a+c=0且a+c=
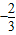 ,
,解得a=
 ,c=-1,
,c=-1,∴f(x)=
 x3-x.
x3-x.(2)由(1)得f'(x)=x2-1,
当x∈[-1,1]时,f'(x)∈[-1,0]
当且仅当x=0时,f'(x)=-1
故?x1,x2∈[-1,0]
f'(x1)•f'(x2)≥0恒成立,
即f'(x1)•f'(x2)≠-1恒成立,
故当x∈[-1,1]时,图象上不存在两点,使得过此两点处的切线互相垂直
点评:本题考查的知识点是函数在某点取得极值的条件,利用导数研究函数曲线上某点的切线方程,其中熟练掌握导数法求函数极值和切线斜率的方法是解答的关键.

练习册系列答案
相关题目
 设函数f(x)=(a
设函数f(x)=(a| x |
| 1 | ||
|
| ∫ | 2π π |
A、-
| ||
| B、-160 | ||
| C、160 | ||
| D、20 |