题目内容
圆心在y轴上,半径为1,且过点(1,2)的圆的方程为( )
| A.x2+(y-2)2=1 | B.x2+(y+2)2=1 |
| C.(x-1)2+(y-3)2=1 | D.x2+(y-3)2=1 |
A
解析

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
直线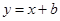 与曲线
与曲线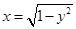 有且仅有1个公共点,则b的取值范围是( )
有且仅有1个公共点,则b的取值范围是( )
A.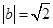 | B. 或 或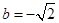 |
C.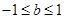 | D.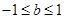 或 或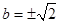 |
若直线 始终平分圆
始终平分圆 的周长,则
的周长,则 的取值范围是( )
的取值范围是( )
| A.(0,1) | B.(0,-1) | C.(-∞,1) | D.(-∞,-1) |
已知点A(﹣3,0),B(0,3),若点P在圆x2+y2﹣2x=0上运动,则△PAB面积的最小值为( )
| A.6 | B.6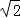 | C.6+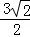 | D.6﹣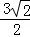 |
已知圆C的圆心是直线x-y+1=0与x轴的交点,且圆C与直线x+y+3=0相切,则圆C的方程为( )
| A.(x+1)2+y2=2 | B.(x-1)2+y2=2 |
| C.(x+1)2+y2=4 | D.(x-1)2+y2=4 |
已知点P(a,b)(ab≠0)是圆x2+y2=r2内的一点,直线m是以P为中点的弦所在的直线,直线l的方程为ax+by=r2,那么( )
| A.m∥l,且l与圆相交 | B.m⊥l,且l与圆相切 |
| C.m∥l,且l与圆相离 | D.m⊥l,且l与圆相离 |
已知圆C的圆心是直线x-y+1=0与x轴的交点,且圆C与直线x+y+3=0相切,则圆C的方程为( )
| A.(x+1)2+y2=2 | B.(x-1)2+y2=1 |
| C.(x+1)2+y2=4 | D.(x-2)2+y2=4 |
当a为任意实数时,直线(a-1)x-y+a+1=0恒过定点C,则以C为圆心,半径为 的圆的方程为( ).
的圆的方程为( ).
| A.x2+y2-2x+4y=0 |
| B.x2+y2+2x+4y=0 |
| C.x2+y2+2x-4y=0 |
| D.x2+y2-2x-4y=0 |


