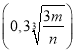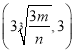Question

【题目】某企业拟生产一种如图所示的圆柱形易拉罐（上下底面及侧面的厚度不计）.易拉罐的体积为 ，设圆柱的高度为 ，底面半径为 ，且.假设该易拉罐的制造费用仅与其表面积有关.已知易拉罐侧面制造费用为元/ ，易拉罐上下底面的制造费用均为元/ （， 为常数，且）.

（1）写出易拉罐的制造费用（元）关于的函数表达式，并求其定义域；

（2）求易拉罐制造费用最低时的值.

Answer 1

【答案】（1）；（2）.

【解析】试题分析：（1）由题意，体积，得，得到函数的解析式，并确定其定义域；

（2）令，求得，确定出函数的单调区间，即可求解函数的最小值.

试题解析：

（1）由题意，体积，得.

.

因为，即，即所求函数定义域为.

（2）令，则.

由，解得.

当时， ，由，

	-	0	+
	减		增

得，当时， 有最小值，此时易拉罐制造费用最低.