题目内容
(本小题满分12分)在a>0时,设命题p:函数y=ax在R上单调递增;命题q:不等式ax2-ax+1>0对x∈R恒成立,若p∧q为假,p∨q为真,求a的取值范围.
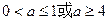
若命题p为真,则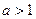 ;若命题q为真,则当
;若命题q为真,则当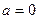 时,不等式即
时,不等式即 恒成立,满足题意;当
恒成立,满足题意;当 时,
时, ,解得
,解得 。由“p∧q为假,p∨q为真”得
。由“p∧q为假,p∨q为真”得 一真一假,又
一真一假,又 ,则
,则 或
或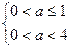 ,解得
,解得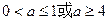 。
。
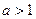 ;若命题q为真,则当
;若命题q为真,则当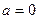 时,不等式即
时,不等式即 恒成立,满足题意;当
恒成立,满足题意;当 时,
时, ,解得
,解得 。由“p∧q为假,p∨q为真”得
。由“p∧q为假,p∨q为真”得 一真一假,又
一真一假,又 ,则
,则 或
或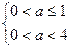 ,解得
,解得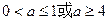 。
。
练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
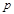 :
: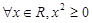 ,则
,则 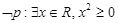
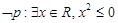
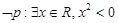
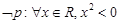
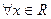 ,
,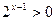
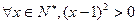
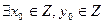 ,使
,使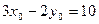
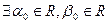 ,使
,使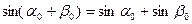
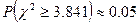 .对此,四名同学做出了如下判断:
.对此,四名同学做出了如下判断: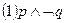 ;
;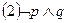 ;
;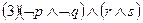 ;
;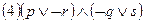 ;
;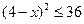 ; q :
; q :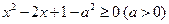 。
。
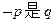 的充分不必要条件,求实数
的充分不必要条件,求实数 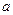 的取值范围。
的取值范围。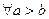 ,都有
,都有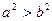 ”的否定是 .
”的否定是 .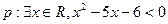 ,则( )
,则( ) 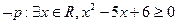
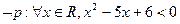
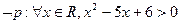
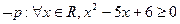
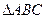 中,若
中,若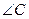 是直角,则
是直角,则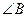 一定是锐角.”的证明过程如下:
一定是锐角.”的证明过程如下: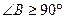 ,
,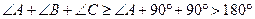 ,
,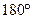 矛盾,所以上述假设不成立,
矛盾,所以上述假设不成立, 恒成立;
恒成立; 中,若
中,若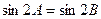 ,则
,则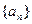 的前n项和
的前n项和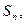 若对任意正整数n都有
若对任意正整数n都有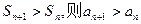 对任意正整数n恒成立;
对任意正整数n恒成立;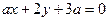 与直线
与直线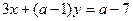 平行且不重合的充要条件;
平行且不重合的充要条件;