题目内容
 (2013•保定一模)设F1、F2分别是椭圆
(2013•保定一模)设F1、F2分别是椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 4 |
| 3 |
(1)求|AF2|•|BF2|的最大值;
(2)若直线l的倾斜角为45°,求△ABF2的面积.
分析:(1)利用椭圆的定义,结合四边形的周长,及|AB|的长,利用基本不等式,即可求|AF2|•|BF2|的最大值;
(2)设出直线l的方程与椭圆方程联立,利用韦达定理及|AB|的长,求出直线方程,即可求△ABF2的面积.
(2)设出直线l的方程与椭圆方程联立,利用韦达定理及|AB|的长,求出直线方程,即可求△ABF2的面积.
解答: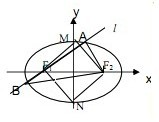 解:(1)∵四边形MF1NF2为菱形,周长为4,∴a=1
解:(1)∵四边形MF1NF2为菱形,周长为4,∴a=1
由椭圆的定义可知|AF2|+|AB|+|BF2|=4a=4,
∵|AB|=
,∴|AF2|+|BF2|=
∴|AF2|•|BF2|≤(
)2=
当且仅当|AF2|=|BF2|=
时,等号成立,即|AF2|•|BF2|的最大值为
;
(2)∵直线l的倾斜角为45°,∴可设l的方程为y=x+c,其中c=
由(1)知椭圆E的方程为x2+
=1
直线方程代入椭圆方程,化简可得(1+b2)x2+2cx+1-2b2=0
设A(x1,y1),B(x2,y2),则x1+x2=
,x1x2=
∵|AB|=
|x1-x2|=
∴
=(
)2-4×
∴b2=
∴c=
∴l的方程为y=x+
∴F2到l的距离d=1
∴S△ABF2=
|AB|×1=
×
×1=
 解:(1)∵四边形MF1NF2为菱形,周长为4,∴a=1
解:(1)∵四边形MF1NF2为菱形,周长为4,∴a=1由椭圆的定义可知|AF2|+|AB|+|BF2|=4a=4,
∵|AB|=
| 4 |
| 3 |
| 8 |
| 3 |
∴|AF2|•|BF2|≤(
| |AF2|+|BF2| |
| 2 |
| 16 |
| 9 |
当且仅当|AF2|=|BF2|=
| 4 |
| 3 |
| 16 |
| 9 |
(2)∵直线l的倾斜角为45°,∴可设l的方程为y=x+c,其中c=
| 1-b2 |
由(1)知椭圆E的方程为x2+
| y2 |
| b2 |
直线方程代入椭圆方程,化简可得(1+b2)x2+2cx+1-2b2=0
设A(x1,y1),B(x2,y2),则x1+x2=
| -2c |
| 1+b2 |
| 1-2b2 |
| 1+b2 |
∵|AB|=
| 2 |
| 4 |
| 3 |
∴
| 8 |
| 9 |
| -2c |
| 1+b2 |
| 1-2b2 |
| 1+b2 |
∴b2=
| 1 |
| 2 |
∴c=
| ||
| 2 |
∴l的方程为y=x+
| ||
| 2 |
∴F2到l的距离d=1
∴S△ABF2=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
| 2 |
| 3 |
点评:本题考查椭圆的定义,考查基本不等式的运用,考查直线与椭圆的位置关系,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 (2013•保定一模)三棱锥V-ABC的底面ABC为正三角形,侧面VAC垂直于底面,VA=VC,已知其正视图(VAC)的面积为
(2013•保定一模)三棱锥V-ABC的底面ABC为正三角形,侧面VAC垂直于底面,VA=VC,已知其正视图(VAC)的面积为