Question

（2013•保定一模）三棱锥V-ABC的底面ABC为正三角形，侧面VAC垂直于底面，VA=VC，已知其正视图（VAC）的面积为

2

3

，则其左视图的面积为（　　）

• A．

  3

  2

• B．

  3

  6

• C．

  3

  4

• D．

  3

  3

Answer 1

分析：由三视图的画图要求“长对正，高平齐，宽相等”可以找出左视图的宽、高与俯视图的宽、主视图的高的相等关系，进而求出答案．

解答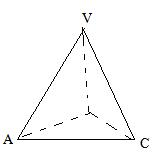：解：设底面正△ABC的边长为a，侧面VAC的底边AC上的高为h，可知底面正△ABC的高为

3

2

a，
∵其主视图为△VAC，∴

1

2

ah=

2

3

；
∵左视图的高与主视图的高相等，
∴左视图的高是h，
又左视图的宽是底面△ABC的边AC上的高

3

2

a，
∴S_侧视图=

1

2

×

3

2

a×h=

3

2

×

2

3

=

3

3

．
故选D．

点评：本题考查了三视图的有关计算，正确理解三视图的画图要求是解决问题的关键．