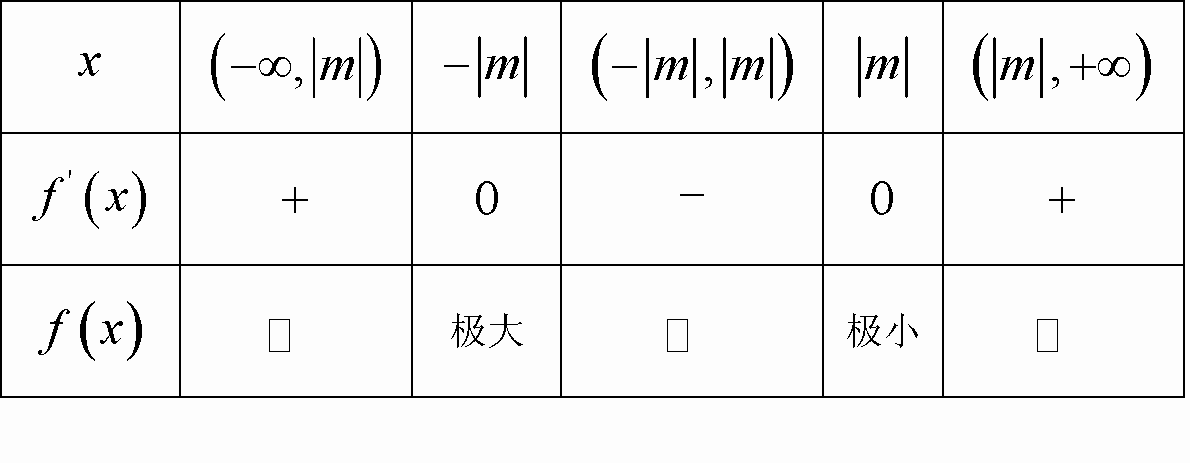
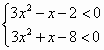题目内容
| |||||||||||
答案:1.导数、解不等式;
解析:
解析:
(1) |
解:由题意 令 对 ∴ 解得 故 |
(2) |
解: ①当 ②当
∴ 又∵ ∴当 当 由题意得 解得 综上, |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
| |||||||||||
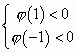 即
即