题目内容
【题目】设 ![]() .
.
(1)讨论函数 ![]() 的极值;
的极值;
(2)当 ![]() 时,
时, ![]() ,求
,求 ![]() 的取值范围.
的取值范围.
【答案】
(1)解: ![]() ,
,
若 ![]() ,则
,则 ![]() ,
, ![]() 在
在 ![]() 上单调递增,没有极值.
上单调递增,没有极值.
若 ![]() ,令
,令 ![]() ,
, ![]() ,列表
,列表
|
|
|
|
|
|
|
|
|
|
|
|
所以当 ![]() 时,
时, ![]() 有极小值
有极小值 ![]() ,没有极大值
,没有极大值
(2)解:由(1)当 ![]() 时,
时, ![]() ,得
,得 ![]() .
.
设 ![]() ,则
,则 ![]()
![]() .从而当
.从而当 ![]() ,即
,即 ![]() 时,
时, ![]()
![]() ,而
,而 ![]() ,于是当
,于是当 ![]() 时,
时, ![]() .
.
由 ![]()
![]() 可得,
可得, ![]() ,即
,即 ![]()
![]() ,从而当
,从而当 ![]() 时,
时, ![]() .故当
.故当 ![]() 时,
时, ![]() ,而
,而 ![]() ,于是当
,于是当 ![]() 时,
时, ![]() .
.
综合得 ![]() 的取值范围为
的取值范围为 ![]() .
.
【解析】(1)求出函数的导函数,通过a与0的大小讨论函数的单调性得到函数的极值。(2)由(1)当a=![]() 时,推出 ex > 1 + x,构造 g(x) 讨论函数的导函数由导函数的性质得出原函数的单调性,即可求出a的取值范围。
时,推出 ex > 1 + x,构造 g(x) 讨论函数的导函数由导函数的性质得出原函数的单调性,即可求出a的取值范围。

练习册系列答案
相关题目
【题目】《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在![]() (不含80)之间,属于酒后驾车,在
(不含80)之间,属于酒后驾车,在![]() (含80)以上时,属于醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了300辆机动车,查处酒后驾车和醉酒驾车的驾驶员共20人,检测结果如下表:
(含80)以上时,属于醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了300辆机动车,查处酒后驾车和醉酒驾车的驾驶员共20人,检测结果如下表:
酒精含量
|
|
|
|
|
|
|
|
|
人数 | 3 | 4 | 1 | 4 | 2 | 3 | 2 | 1 |
(1)绘制出检测数据的频率分布直方图(在图中用实线画出矩形框即可);
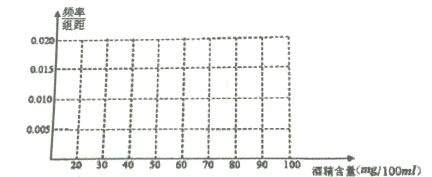
(2)求检测数据中醉酒驾驶的频率,并估计检测数据中酒精含量的众数、平均数.