题目内容
等比数列{an}前n项的积为Tn,若a3a6a18是一个确定的常数,那么数列T10,T13,T17,T25中也是常数的项是( )A.T10
B.T13
C.T17
D.T25
【答案】分析:利用等比数列的通项公式、同底数幂的乘法法则化简a3•a6•a12 =a73 是一个确定的常数,列举出T13的各项,利用
等比数列的性质得到 T13 =a713,即可得到T13为常数.
解答:解:由a3•a6•a18=a1q2•a1q5•a1 q17=(a1 q8)3 =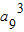 为常数,所以a9为常数,
为常数,所以a9为常数,
则 T17=a1•a2…a17
=(a1•a17)(a2•a16)(a3•a15)(a4•a14)(a5 •a13)(a6•a12)•( a7•a11)•(a8•a10) a9=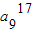 ,
,
为常数.
故选C.
点评:此题主要考查学生灵活运用等比数列的通项公式化简求值,要求学生掌握等比数列的性质,是一道中档题.
等比数列的性质得到 T13 =a713,即可得到T13为常数.
解答:解:由a3•a6•a18=a1q2•a1q5•a1 q17=(a1 q8)3 =
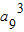 为常数,所以a9为常数,
为常数,所以a9为常数,则 T17=a1•a2…a17
=(a1•a17)(a2•a16)(a3•a15)(a4•a14)(a5 •a13)(a6•a12)•( a7•a11)•(a8•a10) a9=
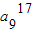 ,
,为常数.
故选C.
点评:此题主要考查学生灵活运用等比数列的通项公式化简求值,要求学生掌握等比数列的性质,是一道中档题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目