题目内容
已知四面体ABCD中,AB=AD=6,AC=4,CD=2
,AB⊥平面ACD,则四面体ABCD外接球的表面积为
| 13 |
88π
88π
.分析:把四面体扩展为长方体,求出长方体的对角线的长,就是外接球的直径,然后求出表面积.
解答: 解:由题意可知几何体是长方体的一部分,如图,
解:由题意可知几何体是长方体的一部分,如图,
长方体的对角线的长为l=
=
=
,就是外接球的直径,
所以外接球的直径为:
,所以球的表面积为:4π(
)2=88π.
故答案为:88π.
 解:由题意可知几何体是长方体的一部分,如图,
解:由题意可知几何体是长方体的一部分,如图,长方体的对角线的长为l=
| AD2+AC2+AB2 |
| 62+42+62 |
| 88 |
所以外接球的直径为:
| 88 |
| ||
| 2 |
故答案为:88π.
点评:本题是基础题,考查几何体的外接球的表面积的求法,考查空间想象能力,计算能力.

练习册系列答案
相关题目
已知四面体ABCD中,AB=2,CD=1,AB与CD间的距离与夹角分别为3与30°,则四面体ABCD的体积为( )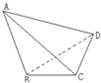

A、
| ||||
| B、1 | ||||
| C、2 | ||||
D、
|
已知四面体ABCD中,AB=AD=6,AC=4,CD=2
,AB⊥平面ACD,则四面体ABCD外接球的表面积为( )
| 13 |
| A、36π | B、88π |
| C、92π | D、128π |
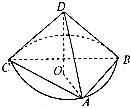 已知四面体ABCD中,DA=DB=DC=3
已知四面体ABCD中,DA=DB=DC=3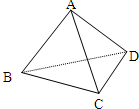 已知四面体ABCD中,
已知四面体ABCD中, 已知四面体ABCD中,DA=DB=DC=3
已知四面体ABCD中,DA=DB=DC=3