题目内容
 已知四面体ABCD中,DA=DB=DC=3
已知四面体ABCD中,DA=DB=DC=3| 2 |
| ||
| 3 |
| ||
| 3 |
分析:当直线DA与直线BC垂直时所成角的余弦值为0,此时两条直线所成的角的余弦值最小,当A在BC与OA平行时,DA与BC所成的角最小.
解答:解:当直线DA与直线BC垂直时所成角的余弦值为0,
此时两条直线所成的角的余弦值最小,
当A在BC与OA平行时,DA与BC所成的角最小.
根据DA=DB=DC=3
,且DA,DB,DC两两互相垂直,得到圆的半径是
,
根据在直角三角形中三角函数的定义得到角的余弦值是
∴直线DA与直线BC所成角的余弦值的取值范围是[0,
]
故答案是
.
此时两条直线所成的角的余弦值最小,
当A在BC与OA平行时,DA与BC所成的角最小.
根据DA=DB=DC=3
| 2 |
| 6 | ||
|
根据在直角三角形中三角函数的定义得到角的余弦值是
| ||
| 3 |
∴直线DA与直线BC所成角的余弦值的取值范围是[0,
| ||
| 3 |
故答案是
| ||
| 3 |
点评:题考查直线与平面所成的角,本题解题的关键是看出两种最值情况下的余弦值,注意在特殊位置的特殊性质的应用.

练习册系列答案
相关题目
已知四面体ABCD中,AB=2,CD=1,AB与CD间的距离与夹角分别为3与30°,则四面体ABCD的体积为( )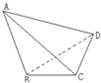

A、
| ||||
| B、1 | ||||
| C、2 | ||||
D、
|
已知四面体ABCD中,AB=AD=6,AC=4,CD=2
,AB⊥平面ACD,则四面体ABCD外接球的表面积为( )
| 13 |
| A、36π | B、88π |
| C、92π | D、128π |
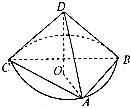 已知四面体ABCD中,DA=DB=DC=3
已知四面体ABCD中,DA=DB=DC=3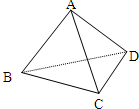 已知四面体ABCD中,
已知四面体ABCD中,