题目内容
已知四面体ABCD中，AB=AD=6，AC=4，CD=2
，AB⊥平面ACD，则四面体ABCD外接球的表面积为（ ）
| 13 |
| A、36π | B、88π |
| C、92π | D、128π |
分析：根据条件构造长方体，求出长方体的对角线的长，就是外接球的直径，然后求出表面积．
解答：解：∵AB=AD=6，AC=4，CD=2
，
∴CD2=AD2+AC2，即DA⊥AC，
∵AB⊥平面ACD，
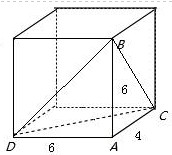
∴四面体ABCD是长方体的一部分，如图，构造长方体，
长方体的对角线的长为l=
=
=2
，
∴长方体的体对角线就是外接球的直径，
外接球的直径2r=2
，
即r=
，
所以球的表面积为：4π（
）2=88π．
故选：B．
| 13 |
∴CD2=AD2+AC2，即DA⊥AC，
∵AB⊥平面ACD，
∴四面体ABCD是长方体的一部分，如图，构造长方体，
长方体的对角线的长为l=
| 62+42+62 |
| 88 |
| 22 |
∴长方体的体对角线就是外接球的直径，
外接球的直径2r=2
| 22 |
即r=
| 22 |
所以球的表面积为：4π（
| 22 |
故选：B．
点评：本题主要考查球的表面积公式，以及球内接长方体的关系，要求熟练掌握长方体的体对角线和球直径之间的关系是解决本题的关键．利用四面体的边长关系构造长方体是解决本题的突破点．
练习册系列答案
相关题目
已知四面体ABCD中，AB=2，CD=1，AB与CD间的距离与夹角分别为3与30°，则四面体ABCD的体积为（ ）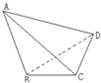
A、
| ||||
| B、1 | ||||
| C、2 | ||||
D、
|
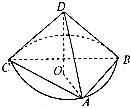已知四面体ABCD中，DA=DB=DC=3
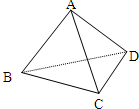已知四面体ABCD中，
已知四面体ABCD中，DA=DB=DC=3