题目内容
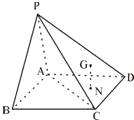 如图,四棱锥P-ABCD的底面ABCD是菱形,∠ABC=60°,△PCD的重心G在底面ABCD上的射影恰好是△ACD的重心N,且GN=
如图,四棱锥P-ABCD的底面ABCD是菱形,∠ABC=60°,△PCD的重心G在底面ABCD上的射影恰好是△ACD的重心N,且GN=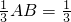 PA=1.
PA=1.
(1)求证:AN⊥PB
(2)求点B到平面PCD的距离
(3)求二面角B-PC-A的大小.
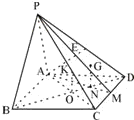 解:(1)证明:∵N是G在面ABCD上的射影,
解:(1)证明:∵N是G在面ABCD上的射影,∴GN⊥面ABCD,又G、N分别为△PCD和△ACD的重心,
∴GN∥PA
∴PA⊥平面ABCD
∴AB为PB在平面ABCD内射影,连PG交CD于点M,则点M为CD的中点,且AN过点M
∵ABCD为菱形,∠ABC=60°,
∴AN⊥CD,又AB∥CD,
∴AN⊥AB,∴AN⊥PB(4分)
(2)∵AB∥CD
∴AB∥平面PCD,
∴点B到面PCD的距离等于点A到面PCD的距离,过点A作AE⊥PM
∴AN⊥CD又PA⊥平面ABCD
∴CD⊥PM
∴CD⊥平面PAM
∴CD⊥AE
∴AE⊥平面PCD
∴AE为点A到平面PCD的距离
∵GN=
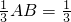 PA=1,∴PA=AB=3,AM=
PA=1,∴PA=AB=3,AM= ,∴PM
,∴PM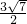
∴AE=
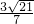 ,
,即点B到平面PCD的距离为
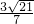 (8分)
(8分)(3)连接BD,过B作BK⊥PC交PC于K,AC与BD交于点O,连KO,易知PC⊥平面KO
∴PC⊥KO,则∠BKO为二面角B-PC-A的平面角
∵AB=3
∴BO=
 ,∴KO=
,∴KO=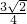
在Rt△BKO中,tan∠BKO=

∴二面角B-PC-A的大小为arttan
 (12分)
(12分)另:用坐标系求解,酌情评分.
分析:(1)N是G在面ABCD上的射影,推出GN⊥面ABCD,GN∥PA,以及PA⊥平面ABCD,连PG交CD于点M,则点M为CD的中点,且AN过点M
证明AN⊥CD,AB∥CD,得到AN⊥PB
(2)说明点B到面PCD的距离等于点A到面PCD的距离,过点A作AE⊥PM
AE⊥平面PCD,然后求出
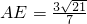 ,即点B到平面PCD的距离为
,即点B到平面PCD的距离为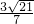 .
.(3)连接BD,过B作BK⊥PC交PC于K,AC与BD交于点O,连KO,说明∠BKO为二面角B-PC-A的平面角
在Rt△BKO中,
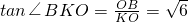 ,二面角B-PC-A的大小为
,二面角B-PC-A的大小为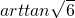 .
.点评:本题是中档题,考查直线与直线的垂直,点到平面的距离,二面角的求法,考查空间想象能力,计算能力,常考题型.

练习册系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=