题目内容
已知函数,对区间(0,1 ]上的任意两个值、,当时总有成立,则的取值范围是
| A.(4,+x) | B.(0,4) | C.(1,4) | D.(0,1) |
A
专题:计算题.
分析:由于x
 <x
<x 时总有f(x
时总有f(x )-f(x
)-f(x )>x
)>x -x
-x 成立,故可将解析式代入,进行整理化简,分离出常数a来,得到a>(x
成立,故可将解析式代入,进行整理化简,分离出常数a来,得到a>(x
 +x
+x
 +x
+x x
x )+1在区间(0,1]上恒成立进而判断出右边式子的最值,得出参数a的取值范围.解答:解:f(x
)+1在区间(0,1]上恒成立进而判断出右边式子的最值,得出参数a的取值范围.解答:解:f(x )-f(x
)-f(x )>x
)>x -x
-x 成立
成立即ax
 1-x
1-x
 -ax2+x
-ax2+x
 >x
>x -x
-x 成立
成立即a(x
 -x
-x )-(x
)-(x -x
-x 1)(x
1)(x
 +x
+x
 +x
+x x
x )>x
)>x 2-x
2-x 成立
成立∵x
 <x
<x ,即x
,即x -x
-x >0
>0∴a-(x

 +x
+x
 +x
+x x
x )>1成立
)>1成立∴a>(x

 +x
+x
 +x
+x x
x )+1在区间(0,1]上恒成立
)+1在区间(0,1]上恒成立当x1x2的值为1时,(x

 +x
+x
 +x
+x x
x )+1的最大值为4,由于x
)+1的最大值为4,由于x <x
<x ≤1故,(x
≤1故,(x
 +x
+x
 +x
+x x
x )+1的最大值取不到4
)+1的最大值取不到4∴a≥4
故选 A
点评:本题考点是函数恒成立的问题,通过对f(x
 )-f(x
)-f(x )>x
)>x -x
-x 进行转化变形,得到关于参数的不等式a>(x
进行转化变形,得到关于参数的不等式a>(x
 +x
+x
 +x
+x x
x )+1在区间(0,1]上恒成立,此种方法是分离常数法在解题中的应用,对此类恒成立求参数的问题,要注意此类技巧的使用.
)+1在区间(0,1]上恒成立,此种方法是分离常数法在解题中的应用,对此类恒成立求参数的问题,要注意此类技巧的使用.
练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
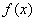 满足
满足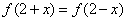 且
且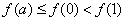 ,则实数
,则实数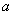 的取值范围是_
的取值范围是_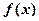 是R上的偶函数,且当
是R上的偶函数,且当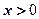 时,函数的解析式为
时,函数的解析式为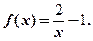
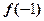 的值;
的值; 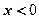 时,函数的解析式;
时,函数的解析式;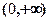 上是减函数;
上是减函数; ,其中
,其中 .定义数列
.定义数列 如下:
如下: ,
, .
. 时,求
时,求 的值;
的值; 的值,若不存在,请说明理由;
的值,若不存在,请说明理由; 时,总能找到
时,总能找到 ,使得
,使得 .
. ,为使每吨平均成本最低,年产量指标应定在多少吨?(注:平均成本
,为使每吨平均成本最低,年产量指标应定在多少吨?(注:平均成本 )
)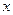 ,当
,当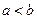 时,二次函数
时,二次函数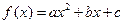 的值恒为非负数,则
的值恒为非负数,则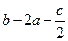 最大值
最大值 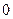 B.
B.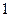 C
C .2 D.
.2 D.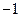
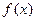 的二次项系数为负,且对任意实数
的二次项系数为负,且对任意实数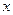 ,恒有
,恒有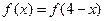 ,若
,若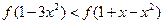 ,则
,则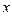 的取值范围是
的取值范围是  为偶函数,其定义域为
为偶函数,其定义域为 ,则
,则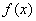 的最小值为( )
的最小值为( )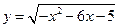 的值域为 ( )
的值域为 ( )


