题目内容
抛物线 在点
在点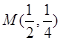 处的切线的倾斜角是 ( )
处的切线的倾斜角是 ( )
A.30 | B.45 | C.60 | D.90 |
B.
解析试题分析:已知抛物线 ,对其进行求导,即
,对其进行求导,即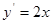 ,当
,当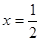 时,
时,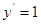 ,即切线的斜率为
,即切线的斜率为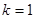 ,从而问题解决.
,从而问题解决.
考点:导数的几何意义;利用导数研究曲线上某点切线方程.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
已知函数 在
在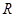 上可导,且
上可导,且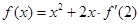 ,则函数
,则函数 的解析式为( )
的解析式为( )
A.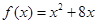 | B.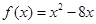 |
C.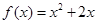 | D.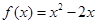 |
定义在R上的函数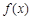 ,若对任意
,若对任意 ,都
,都
有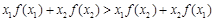 ,则称f(x)为“H函数”,给出下列函数:①
,则称f(x)为“H函数”,给出下列函数:① ;②
;② ;③
;③ ;④
;④ 其中是“H函数”的个数为( ).
其中是“H函数”的个数为( ).
| A.4 | B.3 | C.2 | D.1 |
设函数 在
在 上的导函数为
上的导函数为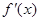 ,
,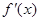 在
在 上的导函数为
上的导函数为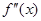 ,若在
,若在 上,
上, 恒成立,则称函数
恒成立,则称函数 在
在 上为“凸函数”.已知当
上为“凸函数”.已知当 时,
时,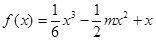 在
在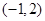 上是“凸函数”.则
上是“凸函数”.则 在
在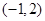 上 ( )
上 ( )
| A.既有极大值,也有极小值 | B.既有极大值,也有最小值 |
| C.有极大值,没有极小值 | D.没有极大值,也没有极小值 |
已知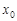 是函数
是函数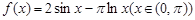 的零点,
的零点,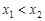 ,则:①
,则:① ;②
;②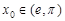 ;
;
③ ;④
;④ ,其中正确的命题是( )
,其中正确的命题是( )
| A.①④ | B.②④ | C.①③ | D.②③ |
已知可导函数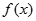 为定义域上的奇函数,
为定义域上的奇函数,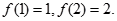 当
当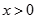 时,有
时,有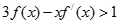 ,则
,则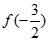 的取值范围为( )
的取值范围为( )
A.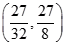 | B.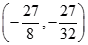 | C.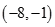 | D.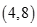 |
设 ,若
,若 ,则
,则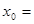 ( )
( )
A.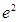 | B. | C.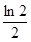 | D. |
函数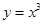 的单调递增区间是( )
的单调递增区间是( )
A.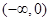 | B. | C.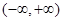 | D.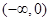 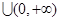 |
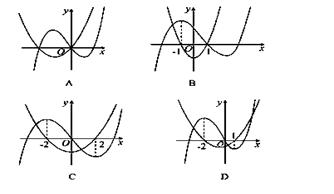
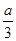 x3+
x3+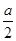 x2-2ax(a≠0)的导函数,则它们的图象可能是 ( )
x2-2ax(a≠0)的导函数,则它们的图象可能是 ( )