题目内容
设函数 在
在 上的导函数为
上的导函数为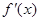 ,
,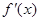 在
在 上的导函数为
上的导函数为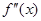 ,若在
,若在 上,
上, 恒成立,则称函数
恒成立,则称函数 在
在 上为“凸函数”.已知当
上为“凸函数”.已知当 时,
时,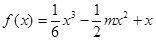 在
在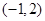 上是“凸函数”.则
上是“凸函数”.则 在
在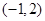 上 ( )
上 ( )
| A.既有极大值,也有极小值 | B.既有极大值,也有最小值 |
| C.有极大值,没有极小值 | D.没有极大值,也没有极小值 |
C
解析试题分析:由题设可知: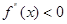 在(-1,2)上恒成立,由于
在(-1,2)上恒成立,由于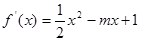 从而
从而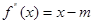 ,所以有
,所以有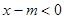 在(-1,2)上恒成立,故知
在(-1,2)上恒成立,故知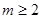 ,又因为
,又因为 ,所以
,所以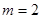 ;从而
;从而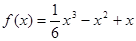 ,
,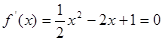 得
得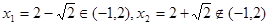 ;且当
;且当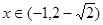 时
时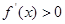 ,当
,当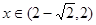 时
时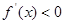 ,所以
,所以 在
在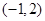 上在
上在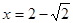 处取得极大值,没有极小值.
处取得极大值,没有极小值.
考点:新定义,函数的极值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
曲线f(x)=x3+x﹣2在p0处的切线平行于直线y=4x﹣1,则p0的坐标为( )
| A.(1,0) | B.(2,8) |
| C.(1,0)或(﹣1,﹣4) | D.(2,8)或(﹣1,﹣4) |
设曲线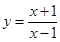 在点
在点 处的切线与直线
处的切线与直线 垂直,则
垂直,则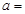 ( )
( )
| A.2 | B.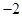 | C. | D. |
定义在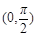 上的函数
上的函数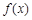 ,
,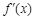 是它的导函数,且恒有
是它的导函数,且恒有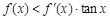 成立,则( )
成立,则( )
A.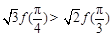 | B.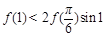 |
C.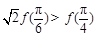 | D.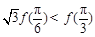 |
曲线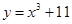 在点
在点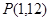 处的切线与
处的切线与 轴交点的纵坐标是( )
轴交点的纵坐标是( )
| A.-9 | B.-3 | C.9 | D.15 |
若 ,则
,则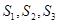 的大小关系为( )
的大小关系为( )
A. | B.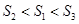 | C.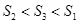 | D.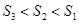 |
抛物线 在点
在点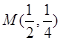 处的切线的倾斜角是 ( )
处的切线的倾斜角是 ( )
A.30 | B.45 | C.60 | D.90 |
已知定义域为R的函数 ,且对任意实数x,总有
,且对任意实数x,总有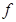 /(x)<3
/(x)<3
则不等式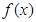 <3x-15的解集为( )
<3x-15的解集为( )
| A.(﹣∞,4) |
| B.(﹣∞,﹣4) |
| C.(﹣∞,﹣4)∪(4,﹢∞) |
| D.(4,﹢∞) |
定义域为R的函数f(x)满足f(1)=1,且f(x)的导函数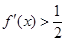 ,则满足
,则满足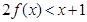 的x的集合为( )
的x的集合为( )
| A.{x|x<1} | B.{x|-1<x<1} | C.{x|x<-1或x>1} | D.{x|x>1} |