题目内容

已知P为抛物线y=x2上的动点,定点A(a,0)关于P点的对称点是Q.

(1)求点Q的轨迹方程;

(2)若(1)中的轨迹与抛物线y=x2交于B、C两点,当AB⊥AC时,求a的值.

解析:(1)设P、Q的坐标分别为(x0,y0)和(x,y),由对称性得x0=,y0=,又y0=x02,

∴=,即y=(x+a)2为所求的轨迹方程.

(2)由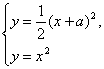得x2-2ax-a2=0,∴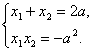∵x1≠x2,∴a≠0.

∵AB⊥AC,∴=-1,即y1y2+x1x2-a(x1+x2)+a2=0.

∵y1·y2=x12·x22=(x1·x2)2=a4,∴a4-a2-2a2+a2=0,即得a=±.

练习册系列答案
相关题目
已知P为抛物线y=2x2+1上的动点，定点A（0，-1），点M分
PA
所成的比为2，则点M的轨迹方程为（　　）
A、y=6x2-
1
3
B、x=6y2-
1
3
C、y=3x2+
1
3
D、y=-3x2-1
已知P为抛物线y=
1
2
x2上的动点，点P在x轴上的射影为M，点A的坐标是(6，
17
2
)，则|PA|+|PM|的最小值是（　　）
A、8
B、
19
2
C、10
D、
21
2
已知P为抛物线y=
1
4
x2上的动点，点P在x轴上的射影为M，点A的坐标是（2，0），则|PA|+|PM|的最小值是
5
-1
5
-1
．
已知P为抛物线y=
1
2
x2上的动点，点P在x轴上的射影为M，点A的坐标是(6，
17
2
)，则|PA|+|PM|的最小值是（　　）
A．8B．
19
2
C．10D．
21
2
已知P为抛物线y=，点P在x轴上的射影为M，点A的坐标是（2，0），则|PA|+|PM|的最小值是    ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网