题目内容
已知P为抛物线y=
x2上的动点,点P在x轴上的射影为M,点A的坐标是(2,0),则|PA|+|PM|的最小值是
-1
-1.
| 1 |
| 4 |
| 5 |
| 5 |
分析:求出抛物线焦点为F(0,1),准线为y=-1,延长PM交准线于N,连接PF,由抛物线定义得|PA|+|PM|=|PA|+|PF|-1,根据三角形两边之和大于第三边,得当P、A、F三点共线时,|PA|+|PF|=|AF|为最小值,由此即可求得|PA|+|PM|的最小值.
解答:解:抛物线y=
x2化成标准形式为x2=4y,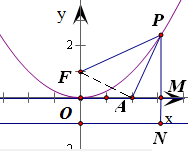
得它的焦点为F(0,1),准线为l:y=-1
延长PM交准线于N,连接PF,根据抛物线的定义,得
|PA|+|PM|=|PA|+|PN|-1=|PA|+|PF|-1
∵△PAF中,|PA|+|PF|>|AF|
∴当且仅当P、A、F三点共线时,|PA|+|PF|=|AF|为最小值
∵|AF|=
=
∴|PA|+|PM|的最小值为
-1
故答案为:
-1
| 1 |
| 4 |

得它的焦点为F(0,1),准线为l:y=-1
延长PM交准线于N,连接PF,根据抛物线的定义,得
|PA|+|PM|=|PA|+|PN|-1=|PA|+|PF|-1
∵△PAF中,|PA|+|PF|>|AF|
∴当且仅当P、A、F三点共线时,|PA|+|PF|=|AF|为最小值
∵|AF|=
| 22+12 |
| 5 |
∴|PA|+|PM|的最小值为
| 5 |
故答案为:
| 5 |
点评:本题给出抛物线上动点,求该点到定点与抛物线准线的距离之和的最小值,着重考查了抛物线的定义和简单几何性质等知识,属于中档题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
已知P为抛物线y=2x2+1上的动点,定点A(0,-1),点M分
所成的比为2,则点M的轨迹方程为( )
| PA |
A、y=6x2-
| ||
B、x=6y2-
| ||
C、y=3x2+
| ||
| D、y=-3x2-1 |