题目内容
(本小题满分12分)在数列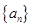 中,
中,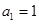 ,
, .
.
(Ⅰ)设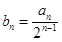 .证明:数列
.证明:数列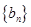 是等差数列;
是等差数列;
(Ⅱ)求数列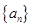 的前
的前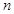 项和
项和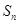 .
.
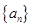 中,
中,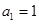 ,
, .
.(Ⅰ)设
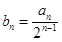 .证明:数列
.证明:数列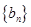 是等差数列;
是等差数列;(Ⅱ)求数列
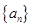 的前
的前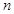 项和
项和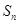 .
.(Ⅰ)见解析;(Ⅱ)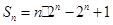
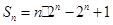
(I)由  ,两边同除以
,两边同除以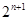 可得
可得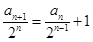 ,然后根据等差数列的定义易证数列
,然后根据等差数列的定义易证数列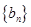 是等差数列.
是等差数列.
(II)先求出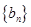 的通项公式,然后可求出
的通项公式,然后可求出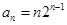 ,显然采用错位相减法求和.
,显然采用错位相减法求和.
解:(1) ,
,
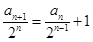 , …………(2分)
, …………(2分)
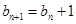 ,
,
则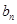 为等差数列,
为等差数列,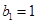 ,…………(4分)
,…………(4分)
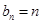 ,
,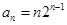 . …………(6分)
. …………(6分)
(2)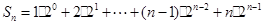 …………(8分)
…………(8分)
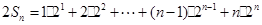 …………(10分)
…………(10分)
两式相减,得
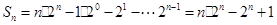 …………(12分)
…………(12分)
 ,两边同除以
,两边同除以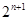 可得
可得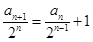 ,然后根据等差数列的定义易证数列
,然后根据等差数列的定义易证数列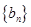 是等差数列.
是等差数列.(II)先求出
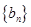 的通项公式,然后可求出
的通项公式,然后可求出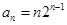 ,显然采用错位相减法求和.
,显然采用错位相减法求和.解:(1)
 ,
,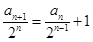 , …………(2分)
, …………(2分)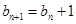 ,
, 则
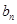 为等差数列,
为等差数列,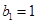 ,…………(4分)
,…………(4分)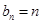 ,
,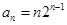 . …………(6分)
. …………(6分)(2)
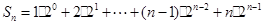 …………(8分)
…………(8分)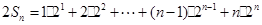 …………(10分)
…………(10分)两式相减,得
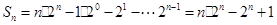 …………(12分)
…………(12分)
练习册系列答案
相关题目
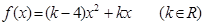 ,对任意实数
,对任意实数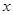 ,
,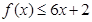 恒成立;正数数列
恒成立;正数数列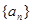 满足
满足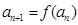 .
.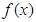 的解析式和值域;
的解析式和值域;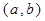 ,使得当
,使得当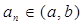 时,数列
时,数列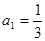 ,求证:数列
,求证:数列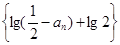 是等比数列
是等比数列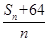 的最小值;
的最小值;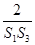 +
+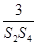 +…+
+…+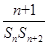 <
<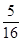 ;
;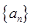 的前项和为
的前项和为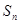 ,且
,且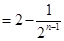 ,
,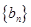 为等差数列,且
为等差数列,且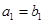 ,
,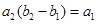
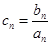 ,求数列
,求数列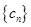 的前
的前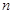 项和
项和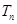 .
. 和等比数列
和等比数列 中,a1=2b1=2,b6=32,
中,a1=2b1=2,b6=32,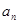 和
和 ;
; ,
,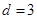 确定的等差数列
确定的等差数列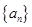 ,当
,当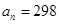 时,序号
时,序号 等于( )
等于( )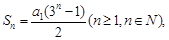 且a4=54,则a1= .
且a4=54,则a1= .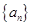 为等差数列,
为等差数列,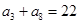 ,
,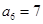 ,则
,则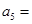 ____________
____________