题目内容
20．
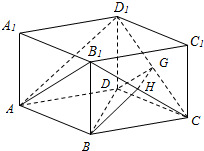已知ABCD-A1B1C1D1 是直四棱拄，其底面是边长为m的菱形，∠BAD=60°，对角面 BDD1B1是矩形，G，H分别是CD1，B1C的中点．（1）求证AD1∥平面BDGH．
（2）若平面ACD1⊥平面ACB1，AA1=2，求m．
分析 （1）设AC∩BD=O，连OG，运用中位线定理和线面平行的判定定理，即可得证；
（2）连OD1，OB1，由二面角的定义，可得∠B1OD1是二面角B1-AC-D1的平面角，即∠B1OD1=90°，再由面面垂直的性质定理和条件，即可得到AB=4．
解答 
（1）证明：设AC∩BD=O，连OG，
∵ABCD为菱形，∴AO=CO，
又G为中点，∴OG∥AD1，OG=$\frac{1}{2}$AD1，
AD1?面BDGH，OG?面BDGH，
∴AD1∥平面BDGH．
（2）解：连OD1，OB1，
∵AD1=CD1，O为AC的中点，
∴OD1⊥AC，同理OB1⊥AC，
∠B1OD1是二面角B1-AC-D1的平面角，
∴∠B1OD1=90°，
作OM⊥B1D1于M，又BDD1B1为矩形，
∴$\frac{OM}{{B}_{1}{D}_{1}}$=$\frac{1}{2}$，即有$\frac{A{A}_{1}}{AB}$=$\frac{1}{2}$，
即AB=4，即m=4．
点评 本题考查线面平行的判定和面面垂直的定义和性质定理的运用，考查二面角平面角的求法，考查运算能力，属于中档题．
练习册系列答案
相关题目
11．设ξ是一个离散型随机变量，其分布列为如下表，则P（2＜ξ≤4）=（ ）
| ξ | 1 | 2 | 3 | … | k | … |
| P | $\frac{1}{2}$ | $\frac{1}{2^2}$ | $\frac{1}{2^3}$ | … | $\frac{1}{2^k}$ | … |
| A． | $\frac{3}{16}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{16}$ | D． | $\frac{5}{16}$ |
15．设随机变量ξ服从B（6，$\frac{1}{2}$），则P（ξ=3）的值是（ ）
| A． | $\frac{5}{8}$ | B． | $\frac{3}{8}$ | C． | $\frac{5}{16}$ | D． | $\frac{3}{16}$ |